Сортування бульбашкою
Сортування обміном або сортування бульбашкою є простим алгоритмом сортування.
 | |
| Клас | Алгоритм сортування |
|---|---|
| Структура даних | Масив |
| Найгірша швидкодія | О(n²) |
| Найкраща швидкодія | О(n) |
| Середня швидкодія | О(n²) |
| Просторова складність у найгіршому випадку | О(n) загальний, O(1) допоміжний |
| Оптимальний | Ні |
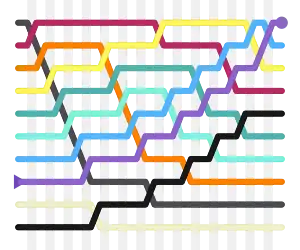
Принцип роботи
Алгоритм працює таким чином — у поданому наборі даних (списку чи масиві) порівнюються два сусідні елементи. Якщо один з елементів, не відповідає критерію сортування (є більшим, або ж, навпаки, меншим за свого сусіда), то ці два елементи міняються місцями. Прохід по списку продовжується доти, доки дані не будуть відсортованими. Алгоритм отримав свою назву від того, що процес сортування за ним нагадує поведінку бульбашок повітря у резервуарі з водою. Оскільки для роботи з елементами масиву він використовує лише порівняння, це сортування на основі порівнянь.
Аналіз
Продуктивність
Складність алгоритму у найгіршому випадку рівна О(n²), де n — кількість елементів для сортування. Існує чимало значно ефективніших алгоритмів, наприклад, з найгіршою ефективністю рівною O(n log n). Тому даний алгоритм має низьку ефективність у випадках, коли N є досить великим, за винятком рідкісних конкретних випадків, коли заздалегідь відомо, що масив з самого початку буде добре відсортований.
Кролики і черепахи
Позиції елементів, що підлягають сортуванню відіграють велику роль у питанні продуктивності даного алгоритму. Великі елементи на початку списку не являють проблему, оскільки вони досить швидко зміщуються на свої місця. Однак, малі елементи у кінці списку переміщуються на його початок дуже повільно. Це призвело до того, що обидва типи елементів було названо кролями і черепахами, відповідно.
З метою підвищення швидкодії алгоритму, у свій час було здійснено чимало зусиль для зменшення кількості «черепах». Сортування перемішуванням є порівняно непоганим, однак, усе ще у своєму найгіршому випадку має складність O(n2). Сортування гребінцем спершу порівнює великі елементи один з одним, а вже тоді поступово переходить до все менших і менших. Його середньостатистична швидкість приблизно рівна такій в алгоритмі Швидке сортування.
Приклад реалізації крок за кроком
Візьмемо масив чисел «5 1 4 2 8», і за допомогою даного алгоритму, відсортуємо його від найменшого до найбільшого елементу. На кожному кроці, елементи, виділені жирним шрифтом будуть порівнюватись.
Перший прохід:
(5 1 4 2 8) (1 5 4 2 8) Тут, алгоритм порівнює перші два елементи, і міняє їх місцями.
(1 5 4 2 8) (1 4 5 2 8)
(1 4 5 2 8) (1 4 2 5 8)
(1 4 2 5 8) (1 4 2 5 8) Тут порівнювані елементи знаходяться на своїх місцях, тож алгоритм не міняє їх місцями.
Після першого проходу масиву найбільший елемент гарантовано опинився на останній позиції, тому в подальшому можна виключити її з роботи.
Другий прохід:
(1 4 2 5 8) (1 4 2 5 8)
(1 4 2 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8) Після другого проходу два найбільших елементи масиву гарантовано опинилися на своїх позиціях, тому в подальшому можна виключити їх з роботи.
Тепер наш масив повністю відсортований, однак, алгоритм цього ще не знає. Йому потрібен ще один «пустий» прохід, під час якого він не поміняє місцями жодного елементу.
Третій прохід:
(1 2 4 5 8) (1 2 4 5 8)
(1 2 4 5 8) (1 2 4 5 8)
Нарешті, масив відсортовано, і алгоритм може припинити свою роботу.
Реалізація
Алгоритм можна виразити як (масив зі стартовим індексом 0):
процедура бульбашка( A : список елементів придатних для сортування )
повторювати
переставлені = хиба
для i = 1 включно до довжина(A) - 1 робити:
/* якщо ця двійка невпорядкована */
якщо A[i-1] > A[i] тоді
/* поміняти місцями і запам'ятати, що щось змінилось */
переставити( A[i-1], A[i] )
переставлені = істина
кінець якщо
кінець для
доки не переставлені
кінець процедуриНа практиці
Хоча алгоритм є одним із найпростіших алгоритмів сортування, його ефективність є досить низькою, і він погано підходить для сортування великих списків. Більшість інших алгоритмів з такою ж швидкодією O(n2) є ефективнішими за алгоритм сортування бульбашками, наприклад, сортування включенням.
Через свою простоту алгоритм часто використовується для пояснення студентам концепції алгоритмів, зокрема алгоритмів сортування. Однак деякі дослідники, як то Оуен Астрахан (Owen Astrachan), ретельно дослідивши даний алгоритм, стверджують, що він настільки поганий і неефективний, що вони навіть не використовуватимуть його як приклад у своїй викладацькій діяльності.[1]
Дональд Кнут у своїй знаменитій праці The Art of Computer Programming прийшов до висновку, що «немає жодних підстав рекомендувати використовувати даний алгоритм, окрім хіба що через примітну назву і через те, що він є лідером у кількості цікавих теоретичних проблем», частину з яких він обговорює у своїй праці.
Сортування бульбашкою під час своєї роботи є асимптоматичним еквівалентом алгоритму сортування включенням у своєму найгіршому випадку, однак обидва алгоритми дуже сильно відрізняються кількістю необхідних операцій переміщення. Результати низки експериментів, наприклад, проведених Астраханом також підтверджують той факт, що продуктивність алгоритму сортування включенням є значно вищою. Тому багато сучасних посібників з алгоритмів навіть не згадують про алгоритм сортування бульбашками і віддають перевагу сортуванню включеннями.
Сортування бульбашкою також погано використовує можливості сучасних мікропроцесорів. Воно вимагає щонайменше удвічі більше операцій, ніж сортування включенням, удвічі більше кешу пам'яті, і асимптоматично більше передбачень переходів. Результати експериментів, проведених Астраханом, показали, що сортування рядка за алгоритмом сортування бульбашками у п'ять разів повільніше за сортування того ж рядка за алгоритмом сортування включенням і на 40% повільніше за сортування вибором.[2]
Примітки
- http://www.cs.duke.edu/~ola/papers/bubble.pdf
- Owen Astrachan. Bubble Sort: An Archaeological Algorithmic Analysis. SIGCSE 2003. (pdf)
Джерела
- Дональд Кнут. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 106–110 of section 5.2.2: Sorting by Exchanging.
- Томас Кормен, Чарльз Лейзерсон, Рональд Рівест, and Кліфорд Стайн. Вступ до алгоритмів, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Problem 2-2, pg.38.
- Sorting in the Presence of Branch Prediction and Caches
Посилання
- Animated Sorting Algorithms: Bubble Sort — графічна демонстрація роботи алгоритму.
- Наочна демонстрація бульбашкового сортування угорськими танцюристами.
- Bubble Sort Demo
- Bubble Sort Demonstration
- Lafore's Bubble Sort
- Sorting Applets in C++
- C++ Program — Bubble Sort
- Analyze Bubble Sort in an online Javascript IDE
- A colored graphical Java applet