Спарені кола Архімеда
У геометрії спарені кола Архімеда — це два спеціальних кола, пов'язані з арбелосом. Арбелос визначається трьома колінеарними точками A, B, та C, і є криволінійною трикутною областю між трьома півколами, діаметрами яких є AB, BC та AC.
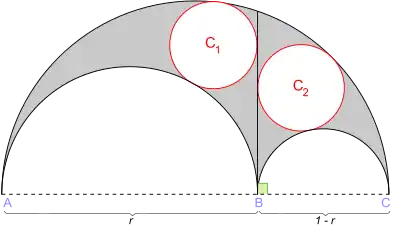
Якщо арбелос розділений на дві менші області відрізком через середню точку A, B й C перпендикулярно лінії ABC, тоді кожен з двох спарених кол Архімеда буде лежати в межах однієї з цих двох областей, дотичної до її двох напівкруглих сторін і до сегмента розщеплення.
Ці кола вперше з'явилися в «Книзі Лем», в якій доводиться (п'яте твердження), що два кола є конгруентними.[1] Сабіт ібн Курра, який переклав цю книгу на арабську мову, приписував її грецькому математику Архімеду. Виходячи з цього твердження, спарені кола Архімеда та кілька інших кіл в арбелосі, які відповідають їм, також називаються колами Архімеда. Однак це приписування було поставлено під сумнів більш пізніми вченими.[2]
Побудова
Зокрема, нехай , , та будуть трьома кутами арбелосу, такими, що розташоване між та . Нехай — точка, в який перетинаються велике півколо та перпендикуляр до проведений через точку . Відрізок ділить арбелос на дві частини. Спареними колами будуть два кола, вписані в ці частини, та кожен з них є дотичним до одного з двох менших півкіл, до відрізку і до великого півкола.[3]
Кожне з двох кіл однозначно визначається трьома дотичними. Їх побудова є окремим випадком задачи Аполлонія. Знайдено також альтернативні підходи до побудови двох кіл, конгруентних спареним колам.[4][5]
Властивості
Нехай a та b — діаметри двох внутрішніх півкіл, так що зовнішнє півколо має діаметр a + b. Діаметр кожного спареного кола потім[3]
Або ж, якщо зовнішнє півколо має діаметр одиниці, а внутрішні кола мають діаметри та , діаметр кожного спареного кола[3]
Найменше коло, що охоплює обидва спарені кола, має ту ж саму площу, що й арбелос.[3]
Інші конгруентні кола
Інші кола, що конгруентні зі спареними колами, також були побудовані з арбелоса. Як і спарені кола, ці кола також називаються архімедовими колами. До них належать коло Банкоффа, кола Шоха та кола Ву.
Див. також
лінія Шоха
Примітки
- Thomas Little Heath (1897), The Works of Archimedes. Cambridge University Press. П'яте твердження у «Книзі Лем». Цитата: "нехай AB-діаметр півкола, C - будь-яка точка на AB і CD, перпендикулярна їй, і нехай півкола описуються в межах першого півкола і мають AC, CB в якості діаметрів. Потім, якщо намалювати два кола, що стикаються з CD з різних сторін, і кожен з них стикається з двома півколами, то намальовані таким чином кола будуть рівні."
- Boas, Harold P. (2006). Reflections on the Arbelos. Mathematical Association of America 113: 241. «Джерелом твердження, що Архімед вивчав і називав арбелос, є «книга Лемм», також відома як "Liber assumptorum" з назви латинського перекладу сімнадцятого століття арабського перекладу дев'ятого століття втраченого грецького оригіналу. Хоча цей збірник з п'ятнадцяти твердженнь включений в стандартні видання праць Архімеда, редактори визнають, що автором «книги Лемм» був не Архімед, а якийсь анонімний пізніший упорядник, який дійсно посилається на Архімеда в третій особі.»
- Weisstein, Eric W. ""Archimedes' Circles." From MathWorld—A Wolfram Web Resource" (анг.). Процитовано 10 квітня 2008.
- Floor van Lamoen (2014). A catalog of over fifty Archimedean circles (анг.). Процитовано 08 жовтня 2014.
- Floor van Lamoen (2014). Circles (A61a) and (A61b): Dao pair (анг.). Процитовано 08 жовтня 2014.