Півколо

Півколо у геометрії — одновимірне геометричне місце точок, які утворюють половину кола. Повна дуга півкола завжди дорівнює 180° (еквівалентно, радіанів, або півоберту). Півколо має тільки одну лінію симетрії (осьової симетрії). Інколи термін «півколо» використовують для позначення півкруга, який являє собою двовимірну геометричну фігуру з внутрішніми точками, обмежену півколом та діаметром, що з'єднує його кінці.

Півколо радіуса r.

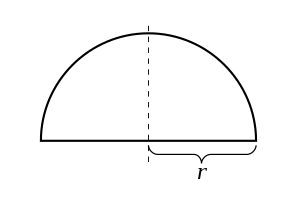
За теоремою Фалеса про три точки на колі, будь-який трикутник, що вписаний у півколо з вершиною в кожному з кінців півкола і третьою вершиною в іншій точці на півколі, є прямокутний трикутник з прямим кутом у третій вершині. Всі лінії, що перетинають півколо перпендикулярно, перетинаються в одній точці в центрі кола, половиною якого є це півколо.

Використання

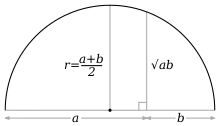
Півколо можна використати для побудови арифметичних і середніх геометричних двох довжин, використовуючи прямий край і циркуль. Якщо ми робимо півколо з діаметром a+b, то довжина його радіуса є середнім арифметичним а+b (оскільки радіус дорівнює половині діаметра). Для того, щоб знайти геометричне середнє, спочатку ділимо діаметр на два відрізки довжин а та b. Потім сполучаємо їхню спільну кінцеву точку з півколом за допомогою відрізка, перпендикулярного до діаметра. Довжина отриманого відрізка і є середнє геометричне. Справедливість цього можна довести використовуючи теорему Піфагора. Цю побудову можна застосувати для визначення квадратури прямокутника (оскільки квадрат, сторони якого дорівнюють середньому геометричному сторін прямокутника, має ту ж площу, що й прямокутник), і, таким чином, будь-якої фігури, для якої можна побудувати прямокутник рівної площі, як наприклад, будь-який багатокутник (але не коло).

Рівняння

Рівняння півкола з серединою на діаметрі, що сполучає його кінці, і яке повністю увігнуте знизу, має вигляд:

.

Якщо півколо повністю увігнуте зверху, то рівняння набуде вигляду:

.

Арбелос

Арбелос — це область на площині, обмежена трьома півколами, з'єднаними в кутах, всі вони на тій самій стороні від прямої лінії (їхня спільна основа), яка містить їхні діаметри.

Див. також

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.