Спрощений алгоритм з обмеженням пам'яті
Спро́щений алгори́тм A* з обмеже́нням па́м'яті (англ. «SMA* (Simplified Memory-Bounded A*) algorithm») — це варіант A* пошуку з обмеженою пам'яттю.
| Алгоритми пошуку графами та деревами |
|---|
|
| Переліки |
|
| Пов'язані теми |
Основна ідея алгоритму
Якщо немає вільного місця, відбирати найменш перспективний вузол з черги, але й відстежувати найкраще забуте значення предка вузла.
Властивості
- Повний — якщо d (глибина оптимального вузла в дереві пошуку) менша за обсягом пам'яті (виражений у вузлах)
- Оптимальний — якщо це рішення можна досягнути
Принцип роботи
Алгоритм SMA* діє повністю аналогічно пошуку A*, розгортаючи найкращі листові вузли до тих пір, поки не буде вичерпана доступна пам'ять. З цього моменту він не може додати новий вузол до дерева пошуку, не знищивши при цьому старий. В алгоритмі SMA* завжди знищується найгірший листовий вузол (той, який має найбільше оцінки). Як і в алгоритмі RBFS, після цього в алгоритмі SMA* значення забутого (знищеного) вузла резервується в його батьківському вузлі. Завдяки цьому предок забутого піддерева дозволяє визначити якість найкращого шляху в цьому піддереві. Оскільки є дана інформація, в алгоритмі SMA* піддерево відновлюється, тільки якщо виявляється, що всі інші шляхи виглядають менш перспективними у порівнянні з забутим шляхом.
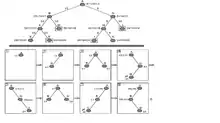
На зображенні продемонстровано приклад роботи алгоритму для дерева з трьох вузлів, який реалізовано за вісім кроків.
Якщо всі листові вузли мають однакове f-значення оцінки? В такому разі може виявитися, що алгоритм вибирає для видалення і розгортання один і той самий вузол. В алгоритмі SMA* ця проблема вирішується шляхом розгортання найновішого найкращого листового вузла і видалення найстаршого найгіршого листового вузла. Ці два вузли можуть виявитися одним і тим самим вузлом, тільки якщо існує лише один листовий вузол; в такому випадку поточне дерево пошуку повинно являти собою єдиний шлях від кореня до листового вузла, що заповнює всю пам'ять. Це означає, що якщо даний листовий вузол не є цільовим вузлом, то рішення недосяжно при доступному обсязі пам'яті, навіть якщо цей вузол знаходиться на оптимальному шляху вирішення. Тому такий вузол може бути відкинутий точно так само, як і в тому випадку, якщо він не має нащадків.
Алгоритм пошуку SMA* можна представити у вигляді псевдокоду
function SMA-star(problem): path queue: set of nodes, ordered by f-cost; begin queue.insert(problem.root-node); while True do begin if queue.empty() then return failure; node := queue.begin(); // мінімальне f-значення вузла if problem.is-goal(node) then return success; s := next-successor(node) f(s) := max(f(node), g(s) + h(s)) if no more successors then update node-s f-cost and those of its ancestors if needed if node.successors ⊆ queue then queue.remove(node); if memory is full then begin badNode := queue.popEnd(); // видаляємо вузли з найвищим f-значенням з черги for parent in badNode.parents do begin parent.successors.remove(badNode); if needed then queue.insert(parent); end; end; queue.insert(s); end; end;
Застосування
З точки зору практики алгоритм SMA* цілком може виявитися найкращим алгоритмом загального призначення для пошуку оптимальних рішень, особливо якщо простір станів являє собою граф, вартості етапів не однакові, а операція формування вузлів є більш дорогою в порівнянні з додатковими витратами супроводу відкритих і закритих списків.
Однак при вирішенні дуже складних завдань часто виникають ситуації, в яких алгоритм SMA* змушений постійно перемикатися з одного шляху вирішення на інший в межах множини можливих шляхів вирішення, і в пам'яті може поміститися тільки невелика підмножина цієї множини. В такому випадку на повторне формування одних і тих же вузлів витрачається додатковий час, а це означає, що завдання, які були б фактично можна вирішити за допомогою пошуку А * при наявності необмеженої пам'яті, стають важковирішуваними для алгоритму SMA*. Іншими словами, через обмеження в обсязі пам'яті деякі завдання можуть ставати важковирішуваними з точки зору часу обчислення. Хоча відсутня теорія, що дозволяє знайти компроміс між витратами часу і пам'яті, створюється враження, що часто уникнути виникнення цієї проблеми неможливо. Єдиним способом подолання такої ситуації стає часткова відмова від вимог до оптимальності рішення.
Див. також
- A*
- D*
- IDA*
- Список алгоритмів
Джерела
1. Russell, S. 1992. Efficient memory-bounded search methods. In Proceedings of the 10th European Conference on Artificial intelligence (Vienna, Austria). B. Neumann, Ed. John Wiley & Sons, New York, NY, 1-5.