Статично невизначувана система

Розрахункова схема статично невизначуваної нерозрізної балки з чотирма опорами

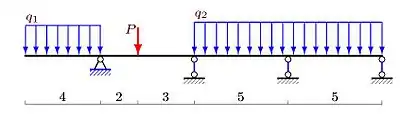
У порівнянні із статично визначуваними системами, у статично невизначуваних системах є додаткові в'язі, що називають зайвими (надлишковими). Необхідною і достатньою ознакою статично невизначуваної системи є наявність надлишкових в'язей, які можна видалити без порушення геометричної незмінності системи.

Термін «зайві в'язі» є умовним. Ці в'язі є зайвими з точки зору розрахункових передумов. У дійсності вони створюють додаткові резерви для конструкції, як у плані забезпечення її механічної жорсткості, так і міцності.

Різниця між кількістю невідомих зусиль і кількістю незалежних (значущих) рівнянь рівноваги, що пов'язують ці зусилля, називається ступенем статичної невизначеності системи, яка розглядається.

У загальному випадку під n-разів статично невизначуваною системою розуміється система, в якій число невідомих зовнішніх опорних реакцій і внутрішніх зусиль перевищує число незалежних і значущих рівнянь рівноваги на n одиниць.

В елементах статично невизначуваних систем (на відміну від статично визначуваних) можуть виникати зусилля, викликані осіданням опор, температурними впливами, усадкою матеріалу, неточністю складання або виготовлення тощо. Розподіл сил у статично невизначуваних системах залежить не лише від навантаження, але і від співвідношення поперечних розмірів окремих елементів, а якщо ці елементи виготовлені з різних матеріалів, то і від співвідношення їх модулів пружності. Якщо у статично визначуваних системах руйнування хоча б однієї в'язі призводить до виходу з ладу усієї споруди, то статично невизначувані системи після втрати однієї або навіть усіх зайвих в'язей зберігають свою тримкість (геометричну незмінність). У цьому сенсі статично невизначувані системи є надійнішими, ніж статично визначні.

Розглянемо плоску задачу. Необхідна для рівноваги кількість накладених в'язей повинна дорівнювати кількості рівнянь рівноваги − ∑X = 0, ∑Y = 0, ∑M = 0 (тобто, трьом). Якщо плоска система складається з D частин, кожну з яких можна розглядати як жорстке тіло, то кількість параметрів, що визначають положення цієї системи буде дорівнювати 3D. Кожен шарнір, що сполучає дві частини системи, дозволяє лише їх взаємне обертання, усуваючи можливість їх взаємних зміщень − отже він зменшує кількість можливих переміщень системи на дві одиниці. Крім того, кожен опорний стержень та шарнірно-рухома в'язь усуває можливість переміщення системи у відповідному напрямі. Таким чином, підрахувати ступінь статичної невизначеності W системи, що виначається зовнішніми в'язями, можна за наступною формулою:

W = 3D — 2Ш — ШР,

де

D − кількість частин системи, кожна з яких може розглядатись як абсолютно жорстке тіло;

Ш − кількість шарнірів у системі, що сполучають ці жорсткі частини;

ШР − кількість опорних стержнів (шарнірно-рухомих в'язей).

Якщо W=0 — то система є статично визначною. При W<0 — конструкція є статично невизначною системою.

Основними методами розрахунку статично невизначуваних систем є метод сил і метод переміщень, у яких за вихідні (зайві) невідомі приймаються відповідно зусилля або переміщення. Метод, що ґрунтується на виборі однієї частини невідомих у вигляді зусиль, а іншої — у вигляді переміщень, називається змішаним. Головні труднощі при розрахунку статично невизначуваних систем з високим ступенем статичної невизначеності полягає у необхідності складання й розв'язування систем рівнянь з великою кількістю невідомих; застосування ЕОМ дає можливість повністю автоматизувати трудомісткий процес розрахунку. Крім зазначених аналітичних методів при розрахунку особливо складних систем використовуються різноманітні чисельні методи.

Приклад статично невизначуваної системи

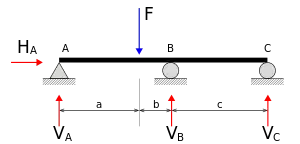
У розрахунковій схемі, поданій на рисунку є чотири невідомі реакції опор: V_A, V_B, V_C і H_A.

Система рівнянь для їх визначення: Сума усіх вертикальних сил дорівнює 0. Σ V = 0:

V_A − F_v + V_B + V_C = 0

Сума усіх горизонтальних сил дорівнює 0. Σ H = 0:

H_A − F_h = 0

Сума усіх моментів сил дорівнює 0. Σ M_A = 0:

F_v • a − V_B • (a + b) — V_C • (a + b + c) = 0.

Так як невідомих чотири (V_A, V_B, V_C і H_A) а рівнянь лише три, то не можливо визначити величини опорних реакцій. Отже система є статично невизначувана. Такі системи можуть бути розраховані з використанням методів опору матеріалів та будівельної механіки, наприклад: рівняння трьох моментів, методу можливих переміщень тощо.

Якщо у розрахунковій схемі прибрати опору B, то реакція V_B зникне, і система стає статично визначуваною.

${\displaystyle H_{A}=F_{h}}$,

${\displaystyle V_{C}={\frac {F_{v}\cdot a}{a+b+c}}}$,

${\displaystyle V_{A}=F_{v}-V_{C}}$.

• Статично визначувана система

• Писаренко Г. С. Опір матеріалів / Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Писаренка Г.С. — К. : Вища школа, 1993. — 655 с. — ISBN 5-11-004-083-4.
• Баженов В. А., Перельмутер А. В., Шишов О. В. Будівельна механіка. Комп'ютерні технології. Підручник. — К. : Каравела, 2009. — 696 с. — ISBN 966-8019-86-5.
• Киселёв В. А. Строительная механика. Общий курс. — М. : Стройиздат, 1986. — 520 с.