Рівняння трьох моментів

Відомо, що балка за наявності додаткових опор стає статично невизначуваною. Одним з методів розрахунку таких балок є метод сил, який полягає у тому, що задана статично невизначувана система звільняється від додаткових в'язей як зовнішніх, так і внутрішніх, а їх дія замінюється силами та моментами сил. Величини цих силових факторів у подальшому підбираються так, щоб переміщення у системі відповідали тим обмеженням, які накладаються на неї відкинутими в'язями. Таким чином, при зазначеному способі розв'язування невідомими виявляються сили. Звідси і назва «метод сил». Такий прийом не є єдино можливим. У будівельній механіці широко застосовуються й інші методи, наприклад метод деформацій (переміщень), у якому за невідомі беруться не силові фактори, а переміщення в елементах стрижневої системи

За допомогою методу сил виводиться рівняння трьох моментів[2]:

${\displaystyle M_{i-1}l_{i}+2M_{i}(l_{i}+l_{i+1})+M_{i+1}l_{i+1}=-6\left({\frac {\Omega _{i}a_{i}}{l_{i}}}+{\frac {\Omega _{i+1}b_{i+1}}{l_{i+1}}}\right).}$

Тут ${\displaystyle \Omega _{i}}$ — площа епюри моментів i-ї статично визначуваної балки; ${\displaystyle a_{i}}$ — відстань від центра ваги i-ї епюри до лівого кінця балки; ${\displaystyle b_{i}}$ — відстань від центра ваги i-ї епюри до правого кінця балки; ${\displaystyle l_{i}=a_{i}+b_{i}}$ — довжина i-ї балки.

Процедура отримання рівняння трьох моментів передбачає, що після уведення шарнірів над опорами отримується статично визначувана система з ${\displaystyle n}$ балок, кожна з яких представляє просту балку з опорами на кінцях. Невідомими у методі сил є моменти сил, прикладені на кінцях незалежних балок. Рівняння трьох моментів встановлює залежність між трьома опорними моментами для двох суміжних прольотів. Для нерозрізної балки кількість таких рівнянь дорівнює кількості проміжних опор балки.

Міст через Сену в Аньєрі (Вінсент ван Гог, 1887)

Вперше рівняння для розрахунку нерозрізних балок застосував мостобудівник й колійний інженер Берто (фр. Bertot) у 1855 році[3]. Сам же метод застосовувався й раніше (1849) при реконструкції моста через Сену в Аньєрі (передмістя Парижа), але опублікований Клапейроном у науковому виданні Академії наук лише у 1857 році[4]. Так як ідея основної системи з невідомими моментами над опорами вперше була висловлена Клапейроном, рівняння трьох моментів пов'язують з його іменем[5]. Подальший розвиток теорія нерозрізних балок отримала у працях Отто Мора, який узагальнив теорію на випадок, коли опори розташовані на різній висоті (1860).

Процедура вирішення задачі з використанням рівняння трьох моментів така.

1. Балка розрізається на окремі частини (прості балки) додатковими внутрішніми шарнірами у місцях кріплення опор.

Позначення реакцій утворених в'язей:

моменти ${\displaystyle M_{0},M_{1},...,M_{n}}$.

2. Нумеруються прогони (ділянки балки між опорами). Кількість прогонів без урахування консолей дорівнює ${\displaystyle n}$. Крайня ліва консоль вважається нульовим прогоном, крайня права має номер ${\displaystyle n+1}$. Довжини прогонів: ${\displaystyle l_{i}}$, ${\displaystyle i=0,...,n+1}$.

3. З умови рівноваги крайніх прогонів (у загальному випадку, консольних частин) визначаються моменти ${\displaystyle M_{0}}$ та ${\displaystyle M_{n}}$. Решта моментів є невідомими системи ${\displaystyle n-1}$ рівнянь трьох моментів.

4. Будуються епюри моментів ${\displaystyle M_{p}}$ та поперечних сил ${\displaystyle Q_{p}}$ у прогонах та консолях (якщо вони є) балки від дії зовнішнього навантаження. Кожен прогін є окремою статично визначуваною балкою.

5. Обчислюються площі епюр моментів ${\displaystyle \Omega _{i}}$, ${\displaystyle i=1,...,n}$ у прогонах та відстані від центрів ваги цих площ до лівої (${\displaystyle a_{i}}$) і правої (${\displaystyle b_{i}}$) опори відповідного прогону.

6. Результати розв'язку системи рівнянь трьох моментів додаються до епюр моментів від зовнішнього навантаження. Отримана епюра і є епюрою моментів у нерозрізній балці.

Побудувати епюру моментів у нерозрізній балці довжиною 19 метрів з чотирма опорами (рис. 1). На балку діє розподілене навантаження ${\displaystyle q_{1}=10}$ кН/м, ${\displaystyle q_{2}=12}$ кН/м та зосереджена сила ${\displaystyle P=9}$ кН.

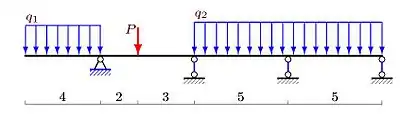
Довжина консолі: ${\displaystyle l_{0}=4}$ м. Довжини прогонів: ${\displaystyle l_{1}=l_{2}=l_{3}=5}$ м.

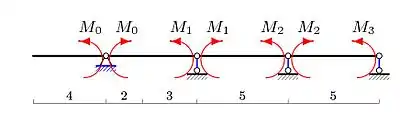
Отримуємо основну систему методу сил, вводячи шарніри над опорами (рис. 2). Моменти ${\displaystyle M_{0}}$ та ${\displaystyle M_{3}}$ — величини відомі й визначаються з умови рівноваги консолей. Правої консолі тут немає, ${\displaystyle M_{3}=0}$. Для лівої консолі отримуємо ${\displaystyle M_{0}=q_{1}l_{0}^{2}/2}$.

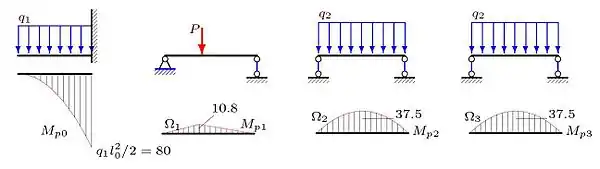
Будуємо епюри моментів від зовнішнього навантаження у незалежних балках основної (статично визначуваної) системи (рис. 3). Епюри побудовані стисненому волокні (як прийнято у машинобудуванні; в будівельній механіці епюри моментів будують на розтягненому волокні).

Записуємо рівняння трьох моментів:

${\displaystyle l_{1}M_{0}+2M_{1}(l_{1}+l_{2})+M_{2}l_{2}=-6(\Omega _{1}a_{1}/l_{1}+\Omega _{2}b_{2}/l_{2}),}$

${\displaystyle l_{2}M_{1}+2M_{2}(l_{2}+l_{3})+M_{3}l_{3}=-6(\Omega _{2}a_{2}/l_{2}+\Omega _{3}b_{3}/l_{3}).}$

Тут ${\displaystyle \Omega _{1}=10.8\cdot 5/2=27,}$ ${\displaystyle a_{1}=(2+5)/3=2.333,}$ ${\displaystyle \Omega _{2}=\Omega _{3}=2fl_{2}/3=125,}$ ${\displaystyle a_{2}=b_{2}=a_{3}=b_{3}=2.5.}$ Розв'язуємо систему рівнянь, звідки: ${\displaystyle M_{1}=7.301}$ кНм, ${\displaystyle M_{2}=-39.325}$ кНм. Будуємо епюру від цих моментів (рис. 4).

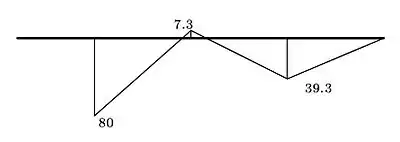
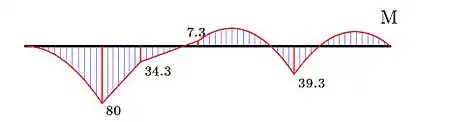
Додаємо (по точках) епюри від навантаження (рис. 3) та від моментів (рис. 4). Отримуємо епюру моментів у балці (рис. 5).

Очевидною перевагою методу є простота матриці системи лінійних рівнянь задачі. Ця матриця є тридіагональною, що дозволяє застосовувати різні спрощені числові методи розв'язування.

• Писаренко Г. С. Опір матеріалів / Г. С. Писаренко, О. Л. Квітка, Е. С. Уманський. За ред. Писаренка Г.С. — К. : Вища школа, 1993. — 655 с. — ISBN 5-11-004-083-4.
• Піскунов В. Г. Опір матеріалів з основами теорії пружності й пластичності : підручник для студ. буд. і транспорт. спец. вузів : У 2. ч. , 5. кн / В. Г. Піскунов. — К., 1994. — Т. 1, кн. 2. — 335 с. — ISBN 5-11-004301-9.
• Киселёв В. А. Строительная механика. Общий курс. — М. : Стройиздат, 1986. — 520 с.

• Методичні вказівки і завдання з опору матеріалів «Розрахунок статично невизначної багатопрогінної балки» (для студентів 2 курсу спец. 6.092108 Теплогазопостачання та вентиляція, 6.092601 Водовідведення та водопостачання) / (Укл. Середа Н. В., Чупринін О. О. — Харків: ХНАМГ, 2006. — 19 с.
• Гребенников М. Н. Расчет многопролетных неразрезных балок. Уравнение трех моментов: учеб. пособие / М. Н. Гребенников, А. Г. Дибир, Н. И. Пекельный. — Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2010. — 46 с.
• The Three-Moment Equation на «αMATHalino.com» (англ.).