Стискна теорема

Стискна теорема (Теорема про двох міліціонерів, Теорема про двох поліцейських) — теорема в математичному аналізі про існування границі у функції, яка «затиснута» між двома іншими функціями, що мають однакову границю. Формальне означення стискної теореми (англ. squeeze theorem) таке:

Нехай I це інтервал, для якого точка a - гранична точка. Нехай f, g і h будуть функціями визначеними на I, можливо окрім точки a. Припустимо, що для кожної точки x в I, яка не дорівнює a, маємо:

$g(x)\leq f(x)\leq h(x)\,$

і також приступне таке:

$\lim _{x\to a}g(x)=\lim _{x\to a}h(x)=L.\,$

Тоді $\lim _{x\to a}f(x)=L.$

Функції g і h називають верхньою та нижньою границями (відповідно) f.
Тут a не мусить бути у внутрішності I. І дійсно, якщо a є кінцевою точкою I, тоді наведені вище границі є лівою або правою границями.
Схоже твердження чинне для нескінченних інтервалів, якщо I = (0, ∞), тоді висновок чинний, з границею при x → ∞.

Доведення

Проведемо доведення із використанням (ε, δ) означення границі, тобто нам потрібно довести, що для кожного дійсного ε > 0 існує дійсне δ > 0 таке, що для всіх x з 0 < |x − a | < δ, виконується -ε <f(x) − L < ε. Тобто,

\forall \varepsilon >0\ \exists \ \delta >0:\forall x\ (0<|x-a|<\delta \ \Rightarrow \ -\varepsilon <f(x)-L<\varepsilon ).

.

Те, що

\lim _{x\to a}g(x)=L

значить, що

\forall \varepsilon >0\ \exists \ \delta 1>0:\forall x\ (0<|x-a|<\delta 1\ \Rightarrow \ -\varepsilon <g(x)-L<\varepsilon ).

(1)

і

\lim _{x\to a}h(x)=L

значить, що

\forall \varepsilon >0\ \exists \ \delta 2>0:\forall x\ (0<|x-a|<\delta 2\ \Rightarrow \ -\varepsilon <h(x)-L<\varepsilon ).

, (2)

тоді ми маємо

g(x)\leq f(x)\leq h(x)\,

g(x)-L\leq f(x)-L\leq h(x)-L\,

Ми можемо обрати δ таке, що δ < δ1 і δ < δ2. Тоді, якщо |x - a|<δ, поєднавши (1) і (2), отримаємо

-\varepsilon <g(x)-L\leq f(x)-L\leq h(x)-L\ <\varepsilon ,

-\varepsilon <f(x)-L<\varepsilon

, що й треба було довести.

Приклад

Перший приклад

x² sin(1/x) затиснута як x прямує до 0

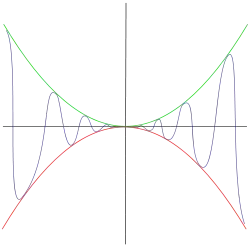
Границю

\lim _{x\to 0}x^{2}\sin({\tfrac {1}{x}})

неможливо встановити через закон

\lim _{x\to a}(f(x)\cdot g(x))=\lim _{x\to a}f(x)\cdot \lim _{x\to a}g(x),

бо

\lim _{x\to 0}\sin({\tfrac {1}{x}})

не існує.

Однак, з визначення синуса,

-1\leq \sin({\tfrac {1}{x}})\leq 1.\,

Випливає, що

-x^{2}\leq x^{2}\sin({\tfrac {1}{x}})\leq x^{2}\,

З того, що $\lim _{x\to 0}-x^{2}=\lim _{x\to 0}x^{2}=0$ , за стискною теоремою, $\lim _{x\to 0}x^{2}\sin({\tfrac {1}{x}})$ повинен бути 0.

Другий приклад

Ймовірно найвідоміші приклади віднайдення границі через затискання — це доведення того, що

{\begin{aligned}&\lim _{x\to 0}{\frac {\sin x}{x}}=1,\\[10pt]&\lim _{x\to 0}{\frac {1-\cos x}{x}}=0.\end{aligned}}

Перший випливає з використання стискної теореми і факти, що

\cos x<{\frac {\sin x}{x}}<1

для x досить близького, але не рівного 0.

Ці дві границі використовуються для доведення того, що похідна синуса є косинус. На цей факт спираються доведення значень похідних для інших тригонометричних функцій.

Посилання

Weisstein, Eric W. Стискна теорема(англ.) на сайті Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.