Твердження Едсгара Дейкстра

Розглянемо довільний трикутник ABC.

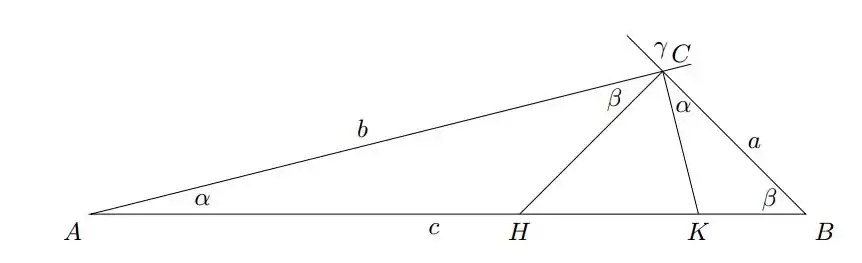
Дейкстра побудував дві додаткові лінії CH і CK так що ${\displaystyle \angle BCK=\angle CAB}$ і ${\displaystyle \angle ACH=\angle CBA}$, що робить трикутники ABC, ACH і BCK подібними і кути AHC і BKC рівними.

Ми маємо випадок ${\displaystyle \alpha +\beta <\gamma }$, в якому трикутники CKB і AHC, непересічні області і не охоплюють весь ${\displaystyle \triangle ACB}$; позначаючи площі ${\displaystyle \triangle XYZ}$ як "XYZ" отримаємо наступний випадок

${\displaystyle CKB+AHC<ACB.}$

У випадку ${\displaystyle \alpha +\beta =\gamma }$, H і K збігаються і ми маємо

${\displaystyle CKB+AHC=ACB}$

і у випадку ${\displaystyle \alpha +\beta >\gamma }$, де два трикутники перетинаються, маємо

${\displaystyle CKB+AHC>ACB.}$

Підсумувавши, отримаємо

${\displaystyle \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(CKB+AHC-ACB).}$

Три площі цих подібних трикутників мають співвідношення як квадрати відповідних сторін, зокрема

${\displaystyle {\frac {CKB}{a^{2}}}={\frac {AHC}{b^{2}}}={\frac {ACB}{c^{2}}}=k>0,\;k>0.}$

Звідси,

${\displaystyle \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(a^{2}+b^{2}-c^{2}).}$

Отже, ми довели теорему

${\displaystyle \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(a^{2}+b^{2}-c^{2}).}$

Розглянемо ${\displaystyle \triangle BOC}$ та ${\displaystyle \triangle DOA}$.

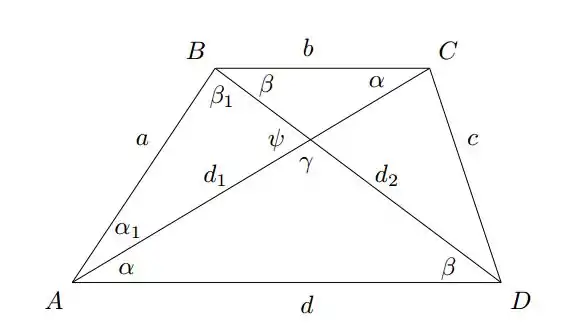
З подібності трикутників маємо відношення

${\displaystyle {\frac {BC}{DA}}={\frac {BO}{DO}}={\frac {CO}{AO}}=k.}$

Нехай ${\displaystyle AC=d_{1}}$, тоді

${\displaystyle {\frac {CO}{AO}}={\frac {d_{1}-AO}{AO}}=k;\;AO={\frac {d_{1}}{k+1}}}$.

Нехай ${\displaystyle BD=d_{2}}$. Аналогічно

${\displaystyle DO={\frac {d_{2}}{k+1}}}$.

За теоремою Дейкстра

${\displaystyle \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(AO^{2}+OD^{2}-AD^{2})=\operatorname {sgn} \left({\frac {d_{1}^{2}}{(k+1)^{2}}}+{\frac {d_{2}^{2}}{(k+1)^{2}}}-d^{2}\right).}$

Відомо, що ${\displaystyle d_{1}^{2}+d_{2}^{2}=2bd+a^{2}+c^{2}}$.

Виразимо d:

${\displaystyle {\frac {BC}{AD}}=k={\frac {b}{d}};\;k+1={\frac {b}{d}}+1={\frac {b+d}{d}}\Longrightarrow d={\frac {b+d}{k+1}}}$.

Підставимо:

${\displaystyle \operatorname {sgn} \left({\frac {2bd+a^{2}+c^{2}}{(k+1)^{2}}}-{\frac {(b+d)^{2}}{(k+1)^{2}}}\right)=\operatorname {sgn} \left({\frac {2bd+a^{2}+c^{2}-b^{2}-2bd-d^{2}}{(k+1)^{2}}}\right)=}$

${\displaystyle =|k+1\neq 0|=\operatorname {sgn}(a^{2}+c^{2}-b^{2}-d^{2})=\operatorname {sgn}(\alpha +\beta -\gamma ).}$

Оскільки ${\displaystyle \gamma =\alpha _{1}+\beta _{1}}$ одержимо наступну рівність

${\displaystyle \operatorname {sgn}(\alpha +\beta -\gamma )=\operatorname {sgn}(\alpha +\beta -\alpha _{1}-\beta _{1})=\operatorname {sgn}(a^{2}+c^{2}-b^{2}-d^{2}).}$

Що й треба було довести.