Signum-функція

Функція знаку y = sgn(x)

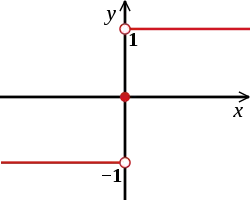
Функція знаку дійсного числа x визначається наступним чином:

${\displaystyle \operatorname {sgn}(x)={\begin{cases}-1,&{\text{якщо }}x<0,\\0,&{\text{якщо }}x=0,\\1,&{\text{якщо }}x>0.\end{cases}}}$

Або як:

${\displaystyle \operatorname {sgn}(x)={\frac {\mathrm {\operatorname {d} } }{\mathrm {\operatorname {d} } x}}\left|x\right|,\quad x\neq 0.}$

Будь-яке дійсне число може бути представлене у вигляді добутку його абсолютного значення і його функції знаку:

${\displaystyle x=\operatorname {sgn}(x)\cdot |x|\,.}$

Звідси випливає, що при${\displaystyle \quad x\neq 0}$

${\displaystyle \operatorname {sgn}(x)={x \over |x|}={|x| \over x}\,.}$

Так само і для будь-якого дійсного числа x

${\displaystyle |x|=\operatorname {sgn}(x)\cdot x\,.}$

Ми також можемо переконатися, що

${\displaystyle \operatorname {sgn}(x^{n})=(\operatorname {sgn}(x))^{n}.}$

Функція ${\displaystyle \operatorname {sgn}(x)}$ є похідною функції ${\displaystyle y=|x|,}$ з точністю до невизначеності при x = 0:

${\displaystyle {\operatorname {d} |x| \over \operatorname {d} x}=\operatorname {sgn}(x){\mbox{ для }}x\neq 0.}$

Більш формально, в теорії інтегрування функцій  — це слабка похідна, а в теорії опуклих функцій субдиференціалом абсолютного значення при ${\displaystyle x=0}$ є інтервал ${\displaystyle [-1,1]}$, «заповнення» функції знаку (субдиференціал абсолютного значення не є однозначним при ${\displaystyle x=0}$).

Функція знаку не є неперервною у точці x = 0

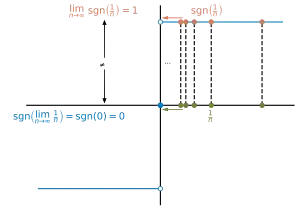
Похідна функції ${\displaystyle \operatorname {sgn}(x)}$ дорівнює 0 для всіх x крім 0. Вона не є диференційовною при ${\displaystyle x=0}$ у звичайному сенсі, але диференційовною в узагальненому сенсі в теорії розподілу, похідною від функції ${\displaystyle \operatorname {sgn}(x)}$ є дельта-функція Дірака, що можна показати за допомогою тотожності

${\displaystyle \operatorname {sgn}(x)=2H(x)-1\,,}$

де H(x) — Функція Гевісайда, H(0) = 12. Використовуючи цю тотожність, легко знайти похідну:

${\displaystyle {\frac {\operatorname {d} (\operatorname {sgn}(x))}{\operatorname {d} x}}=2{\frac {\operatorname {d} H(x)}{\operatorname {d} x}}=2\delta (x)\,.}$

Перетворення Фур'є функції ${\displaystyle \operatorname {sgn}(x)}$ має вигляд

${\displaystyle \int _{-\infty }^{\infty }\operatorname {sgn}(x)e^{-ikx}\operatorname {d} x=\mathrm {p.v.} {\frac {2}{ik}},}$

де p.v. — головне значення інтеграла за Коші.

Функцію ${\displaystyle \operatorname {sgn}(x)}$ також можна виразити за допомогою дужки Айверсона

${\displaystyle \ \operatorname {sgn}(x)=-[x<0]+[x>0]\,.}$

Функцію ${\displaystyle \operatorname {sgn}(x)}$ можна записати з використанням функцій підлоги та абсолютного значення:

${\displaystyle \ \operatorname {sgn}(x)={\Bigg \lfloor }{\frac {x}{|x|+1}}{\Bigg \rfloor }-{\Bigg \lfloor }{\frac {-x}{|-x|+1}}{\Bigg \rfloor }\,.}$

Для k ≫ 1 неперервне наближення функції знаку має вигляд:

${\displaystyle \ \operatorname {sgn} (x)\approx \operatorname {th} (kx)\,.}$

Інше наближення має вигляд:

${\displaystyle \ \operatorname {sgn}(x)\approx {\frac {x}{\sqrt {x^{2}+\varepsilon ^{2}}}}\,,}$

яке стає «гострішим» при ε → 0; зауважимо, що це похідна від функції √x² + ε². Це ґрунтується на тому факті, що ${\displaystyle \ {\frac {x}{\sqrt {x^{2}+\varepsilon ^{2}}}}=\operatorname {sgn}(x)\,}$ для всіх x ≠ 0 якщо ε = 0, і дає переваги для простого узагальнення на багатовимірні аналоги функції знаку (наприклад, частинні похідні функції √x² + y²).

Функцію ${\displaystyle \operatorname {sgn}(x)}$ можна узагальнити на комплексні числа:

${\displaystyle \operatorname {sgn}(z)={\frac {z}{|z|}},}$

для будь-якого комплексного числа z, крім z = 0. Таким чином, значення функції ${\displaystyle \operatorname {sgn}(z)}$ буде точкою на одиничному колі комплексної площини, що найближча до точки z. Тоді для z ≠ 0:

${\displaystyle \operatorname {sgn}(z)=e^{i\arg z}\,,}$

де ${\displaystyle \arg(z)\,}$ — аргумент комплексного числа.

Комплексний варіант

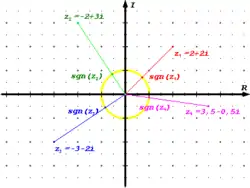
З міркувань симетрії та для належного узагальнення функції ${\displaystyle \operatorname {sgn}(z)}$ на множині дійсних чисел, зазвичай дану функцію на комплексній площині визначають і для z = 0:

${\displaystyle \operatorname {sgn} (0+0i)=0.}$

Іншим узагальненням функції ${\displaystyle \operatorname {sgn}(z)}$ для дійсних і комплексних виразів є функція csgn, що визначається як

${\displaystyle \operatorname {csgn} (z)={\begin{cases}1,&{\text{якщо }}\mathrm {Re} (z)>0\\-1,&{\text{якщо }}\mathrm {Re} (z)<0\\\operatorname {sgn}(\mathrm {Im} (z)),&{\text{якщо }}\mathrm {Re} (z)=0,\end{cases}}}$

де Re(z) — дійсна частина числа z, а Im(z) — комплексна частина z. Тоді для z ≠ 0 маємо

${\displaystyle \operatorname {csgn} (z)={\frac {z}{\sqrt {z^{2}}}}={\frac {\sqrt {z^{2}}}{z}}.}$

Для дійсних значень x можна визначити узагальнену функцію (аналог функції знаку) ε(x), таку, що (ε(x))² = 1 для всіх x, у тому числі і в точці x = 0 (на відміну від функції ${\displaystyle \operatorname {sgn}(x)}$, для якої (sgn(0))² = 0). Ця узагальнена функція дозволяє побудувати алгебру узагальнених функцій, але ціною такого узагальнення є втрата комутативності. Зокрема, узагальнена функція знаку антикомутує з дельта-функцією Дірака

${\displaystyle \varepsilon (x)\delta (x)+\delta (x)\varepsilon (x)=0~;}$

крім цього, ε(x) не можливо визначити при x = 0; і спеціальне позначення ε необхідне, щоб відрізнити її від функції знаку (ε(0) не визначено, але sgn(0) = 0).

• Функція Гевісайда
• Дельта-функція Дірака
• Абсолютне значення
• Від'ємне число
• Сигмоїдна функція
• Прямокутна функція
• Тришляхове порівняння

• Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.