Теорема Бріаншона

Теорема Бріаншона — одна з найважливіших теорем проєктивної геометрії. Названа за іменем французького математика Шарля Жульєна Бріаншона (Charles Julien Brianchon, 1785—1864).

Теорема Бріаншона

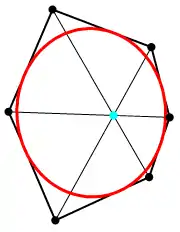
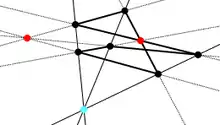
Вона стверджує, що три прямі, які сполучають у пари протилежні вершини шестикутника, описаного навколо конічного перерізу, мають спільну точку, т. з. точку Бріаншона (або паралельні; тоді їх спільна точка безмежно віддалена). Описаний шестикутник утворюється шістьма дотичними, його вершини — точки перетину сусідніх дотичних. Усім можливим нумераціям шести заданих дотичних відповідають 60 шестикутників, отже, 60 точок Бріаншона; вони розміщені по три на двадцяти прямих. Разом з теоремою Паскаля теорема Бріаншона встановлює основні проєктивні властивості конічних перерізів.

Вироджений випадок