Теорема Карно про перпендикуляри
Теорема Карно (названа в честь Лазара Карно) описує необхідну і достатню умову для того, щоб три прямі, перпендикулярні до сторін трикутника (або їх продовжень), перетиналися в одній точці. Теорему також можна розглядати як узагальнення теореми Піфагора.
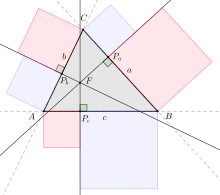
синя площа = червона площа
Теорема
Для трикутника зі сторонами розглянемо три прямі, які перпендикулярні до сторін трикутника і перетинаються в спільній точці . Якщо є точками перетину зазначених трьох прямих зі сторонами трикутника відповідно, то виконується таке рівняння:
Істинним є і обернене твердження, тобто якщо зазначене рівняння виконується для точок перетину трьох прямих, перпендикулярних сторонам, та трьох сторін трикутника, то прямі перетинаються в одній точці. Отже, рівняння вказує на необхідну і достатню умову.
Особливі випадки
Якщо трикутник має прямий кут в точці і точка перетину збігається з будь-якою з точок або , то рівняння, зазначене вище, дає теорему Піфагора. Наприклад, якщо збігається з тоді , , , , і . Отже, наведене вище рівняння перетворюється на теорему Піфагора .
Іншим наслідком теореми Карно про перпендикуляри є властивість перпендикулярних бісектрис трикутника перетинатися в спільній точці. У разі перпендикулярних бісектрис маємо, що , і і, отже, виконується наведене вище рівняння, а це означає, що всі три перпендикуляри перетинаються в одній точці.
Література
- Wohlgemuth, Martin., ред. (2010). Mathematisch für fortgeschrittene Anfänger : Weitere beliebte Beiträge von Matroids Matheplanet (German). Heidelberg: Spektrum Akademischer Verlag. с. 273–276. ISBN 9783827426079. OCLC 699828882.
- Alfred S. Posamentier; Charles T. Salkind (1996). Challenging Problems in Geometry. New York: Dover. с. 85–86. ISBN 9780486134864. OCLC 829151719.
Посилання
- Флоріан Модлер: Vergessene Sätze am Dreieck — Der Satz von Carnot на matheplanet.com (нім.)
- Теорема Карно на cut-the-knot.org (англ.)