Теорема Кейсі

Теорема Кейсі — теорема в геометрії Евкліда, що узагальнює нерівність Птолемея. Названа за іменем ірландського математика Джона Кейсі.

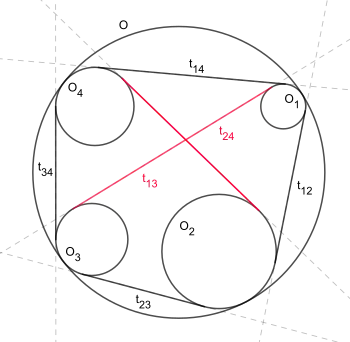
t_{12}\cdot t_{34}+t_{14}\cdot t_{23}=t_{13}\cdot t_{24}.

Формулювання

Нехай $O$ — коло радіуса $R$ . Нехай $O_{1},O_{2},O_{3},O_{4}$ — (в зазначеному порядку) чотири кола, що не перетинаються, які лежать всередині $O$ і дотичні до нього. Позначимо через $t_{ij}$ довжину відрізка між точками дотику зовнішньої спільної дотичної кіл $O_{i},O_{j}$ . Тоді[1]:

t_{12}\cdot t_{34}+t_{14}\cdot t_{23}=t_{13}\cdot t_{24}.

У виродженому випадку, коли всі чотири кола зводяться до точок (кіл радіуса 0), виходить точно теорема Птолемея.

Зауваження

Теорема Кейсі справедлива для шести попарних дотичних чотирьох кіл, що дотичні до одного спільного кола не тільки внутрішньо, як розібрано вище, але й зовнішньо, як показано на рисунку нижче.

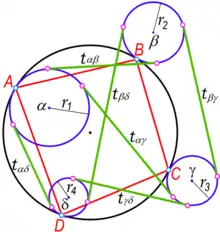
Теорема Кейсі

При цьому виконується звичайна формула теореми Кейсі:

t_{\alpha \beta }t_{\gamma \delta }+t_{\beta \gamma }t_{\delta \alpha }=t_{\alpha \gamma }t_{\beta \delta }

.

У виродженому випадку, коли три з чотирьох кіл зводяться до точок (кіл радіуса 0), і одна сторона чотирикутника вироджується в точку, а три сторони чотирикутника, що залишилися утворюють рівносторонній трикутник, виходить точно узагальнена теорема Помпею.
У виродженому випадку, коли всі чотири кола зводяться до точок (кіл радіуса 0), в останньому випадку також виходить теорема Птолемея.

Примітки

Casey, 1866.

Джерела

John Casey. On the Equations and Properties: (1) of the System of Circles Touching Three Circles in a Plane; (2) of the System of Spheres Touching Four Spheres in Space; (3) of the System of Circles Touching Three Circles on a Sphere; (4) of the System of Conics Inscribed to a Conic, and Touching Three Inscribed Conics in a Plane // Proceedings of the Royal Irish Academy. — 1866. — № 9. — С. 396—423.
M. Zacharias. Der Caseysche Satz // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1942. — Т. 52. — С. 79—89.
O. Bottema. Hoofdstukken uit de Elementaire Meetkunde. — of the second extended edition published by Epsilon-Uitgaven 1987. — Springer 2008 (translation by Reinie Erné as Topics in Elementary Geometry), 1944.
Roger A. Johnson. Modern Geometry. — Houghton Mifflin, Boston (republished facsimile by Dover 1960, 2007 as Advanced Euclidean Geometry), 1929.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTECasey1866-1] Casey, 1866.