Теорема Паппа про площі

Нехай задано довільний трикутник з двома довільними паралелограмами, побудованими на цих сторонах.

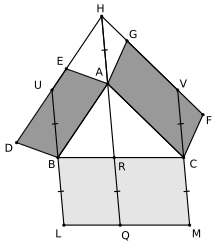
Теорема показує як побудувати паралелограм на третій стороні так, щоб його площа дорівнювала сумі площ інших двох паралелограмів. Нехай ABC довільний трикутник, ABDE і ACFG — два довільних паралелограми, побудованих на двох його сторонах AB і AC. Продовжимо сторони DE і FG до їх перетину в точці H. Тоді відрізок AH використовується для побудови третього паралелограма BCML на стороні BC, тобто будуються відрізки BL та CM, причому BL = CM = AH і ${\displaystyle BL\parallel CM\parallel AH}$. Тоді виконується наступна тотожність для площ паралелограмів:

${\displaystyle {\text{S}}_{ABDE}+{\text{S}}_{ACFG}={\text{S}}_{BCML}}$.

Теорема Паппа узагальнює теорему Піфагора двояко. По-перше, теорему можна використовувати для довільних трикутників, а не лише для прямокутних. По-друге, теорема використовує паралелограми, а не квадрати. Для квадратів побудованих на двох сторонах довільного трикутника теорема визначає відповідний паралелограм на третій стороні, площа якого дорівнює сумі площ квадратів, а у випадку, якщо дві сторони утворюють прямий кут, то паралелограм на третій стороні також буде квадратом. Для прямокутного трикутника два паралелограми побудовані на катетах прямого кута визначають прямокутник побудований на третій стороні, і знову, якщо два паралелограми є квадратами, то прямокутник побудований на третій стороні також буде квадратом.

Завдяки тому, що паралелограми ABDE і ABUH мають спільну сторону і висоту, то вони мають однакові площі. Аналогічні міркування використовуємо щодо паралелограмів ACFG і ACVH, ABUH і BLQR, ACVH і RCMQ. Це дає бажаний результат, оскільки

${\displaystyle {\begin{aligned}{\text{S}}_{ABDE}+{\text{S}}_{ACFG}&={\text{S}}_{ABUH}+{\text{S}}_{ACVH}\\&={\text{S}}_{BLRQ}+{\text{S}}_{RCMQ}\\&={\text{S}}_{BCML}.\end{aligned}}}$

• Теорема Паппа
• Теореми Паппа — Гульдіна

• The Pappus Area Theorem
• Pappus theorem

• Howard Eves: Pappus's Extension of the Pythagorean Theorem.The Mathematics Teacher, Vol. 51, No. 7 (November 1958), pp. 544–546 (JSTOR)
• Howard Eves: Great Moments in Mathematics (before 1650). Mathematical Association of America, 1983, ISBN 9780883853108, p. 37 (excerpt, с. 37, на «Google Books»)
• Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press, 2007, ISBN 9780691125268, pp. 58–59 (excerpt, с. 58, на «Google Books»)
• Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 77–78 (excerpt, с. 77, на «Google Books»)