Точка перегину
Точкою перегину кривої називається точка кривої в якій змінюється знак кривини. Якщо крива є графіком функції, то в цій точці опукла частина функції відділяється від ввігнутої.
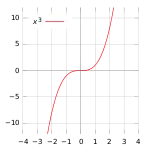
Для функції y = x³ точка перегину (0,0)
Властивості
- Якщо в деякому околі точки перегину a існує перша похідна, то вона є також точкою екстремуму для f′(x).
- Якщо в деякому околі також існує похідна другого порядку то достатньою умовою того, що a — точка перегину є зміна знаку другої похідної в цій точці.
- Якщо в точці перегину існує дотична, то вона перетинає криву в даній точці. Іноді цю властивість використовують як означення точки перегину, однак з виконання цієї властивості не випливає властивість з означення точки перегину. Прикладом цього може бути функція:
Значення другої похідної в точці x=0 для цієї функції рівне нулю, отже дотичною в нулі буде пряма y=0. Ця пряма також перетинає графік функції в точці дотику, однак точка x=0 не є точкою перегину оскільки в довільному околі цієї точки знак другої похідної міняється нескінченну кількість разів.
Класифікація
Точки перегину можна класифікувати в залежності від того чи рівна нулю похідна f′(x) .
- якщо f′(x) рівна нулю, точка називається стаціонарною точкою перегину, або сідловою точкою
- якщо f′(x) не рівна нулю, точка називається нестаціонарною точкою перегину
Прикладом стаціонарної точки є точка (0;0) на графіку функції y = x3. Прикладом нестаціонарної точки є точка (0;0) на графіку функції y = x + x3.
Література
- Фихтенгольц Г. М. Основы математического анализа. — 7-е изд. — М.: ФИЗМАТЛИТ, 1969. — Т. 1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.