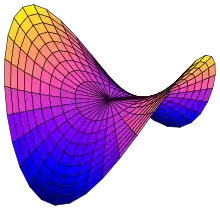
Сідлова точка
Сідлова́ то́чка у математиці або точка мінімакса[1] — це точка на поверхні графіка функції, де всі нахили (похідні) в ортогональних напрямках дорівнюють нулю (тобто, є критичною точкою), але яка не є локальним екстремумом функції[2]. Прикладом сідлової точки є критична точка з відносним мінімумом вздовж одного осьового напрямку (між піками) і відносним максимумом вздовж іншої осі. Однак, сідлова точка не обов'язково має бути в такому вигляді. Наприклад, функція має критичну точку в — це сідлова точка, оскільки вона не є ні відносним максимумом, ні відносним мінімумом, але вона не має відносного максимуму чи відносного мінімуму в напрямку вісі .

Назва походить від того факту, що прототипний приклад у двох вимірах є поверхнею, яка вигинається вгору в одному напрямку і вигинається вниз в іншому напрямку, нагадуючи сідло для верхової їзди або гірський перевал між двома вершинами, що утворюють сідло рельєфу. З точки зору ліній контуру, сідлова точка в двох вимірах створює контурний графік або трасу, на якій контур, що відповідає значенню сідлової точки, здається, перетинає сам себе.
Визначення
Простим критерієм для перевірки того, чи є дана стаціонарна точка дійсної функції F(x, y) двох дійсних змінних сідловою точкою, є обчислення матриці Геса функції в цій точці: якщо гесіан невизначений, то ця точка є сідловою. Наприклад, матриця Гесе функції у стаціонарній точці є матрицею
яка є невизначеною. Тому ця точка є сідловою. Цей критерій дає лише достатню умову. Наприклад, точка є сідловою точкою для функції але матриця Гесе цієї функції в початку координат є нульовою матрицею, яка не є невизначеною.
У найзагальніших термінах сідлова точка для гладкої функції (графіком якої є крива, поверхня або гіперповерхня) є стаціонарною точкою, такою, що крива/поверхня/і т. д. в околі цієї точки не знаходиться повністю по один бік від дотичного простору в цій точці.
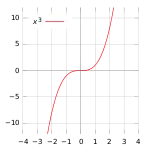
В одновимірному просторі сідловою точкою є точка, яка одночасно є стаціонарною точкою і точкою перегину. Оскільки, це точка перегину, то вона не буде локальним екстремумом.
Сідлова поверхня

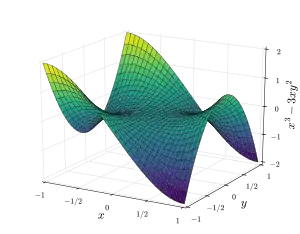
Сідлова поверхня — це гладка поверхня, що містить одну або кілька сідлових точок.
Класичними прикладами двовимірних сідлових поверхонь в евклідовому просторі є поверхні другого порядку, гіперболічний параболоїд (який часто називають «поверхнею сідла» або «стандартною сідловою поверхнею») і однопорожнинний гіперболоїд. Картопляні чіпси Pringles є прикладом гіперболічної параболоїдної форми, який можна зустріти у повсякденному житті.
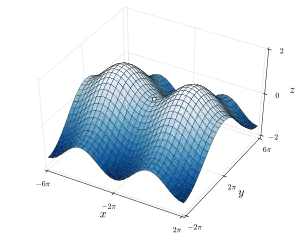
Сідлові поверхні мають від'ємну гаусову кривину, що відрізняє їх від опуклих/еліптичних поверхонь, які мають додатню гаусову кривину. Класичною поверхнею сідла третього порядку є мавпяче сідло[3].
Приклади
У грі з нульовою сумою для двох гравців, визначеній на неперервному просторі, точка рівноваги є сідловою точкою.
Для лінійної автономної системи другого порядку критична точка є сідловою точкою, якщо характеристичне рівняння (диференціальні рівняння) має одне додатне та одне від'ємне дійсне власне значення[4].
При оптимізації з урахуванням обмежень рівності умови першого порядку описують сідлову точку лагранжіана.
Інше використання
У динамічних системах, якщо динаміка задається диференційовною функцією f, точка є гіперболічною тоді й тільки тоді, коли диференціал ƒn (де n — період точки) не має власного значення на (комплексному) одиничному колі при обчисленні у точці. Тоді сідловою точкою є гіперболічна періодична точка, для якої стійкі та нестійкі многовиди мають розмірність, яка не дорівнює нулю.
Сідловою точкою матриці є елемент, який одночасно є найбільшим елементом у своєму стовпці і найменшим елементом у своєму рядку.
Дисипативні системи
Для дисипативної системи, яка описується кінетичними рівняннями
- ,
стаціонарна точка (точка рівноваги) визначається з системи рівнянь
- ,
а її стабільність визначається тим, чи матриця додатньо визначена. Задача аналогічна аналізу екстремуму функції багатьох змінних. Сідлові точки в синергетиці, яка вивчає дисипативні системи, відповідають нестійким стаціонарним станам: вузлам і фокусам.
Аналіз стаціонарних точок дисипативних систем стає зовсім аналогічним аналізу точки екстремуму, якщо існує така функція (потенціал), що
- .
У загальному випадку це не так.
Див. також
- Сідло
- Білінійна форма
- Екстремум
- Мавпяче сідло
Примітки
- Howard Anton, Irl Bivens, Stephen Davis (2002): Calculus, Multivariable Version, p. 844.
- Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (вид. 3rd). New York: McGraw-Hill. с. 312. ISBN 0-07-010813-7.
- Buck, R. Creighton (2003). Advanced Calculus (вид. 3rd). Long Grove, IL: Waveland Press. с. 160. ISBN 1-57766-302-0.
- von Petersdorff, 2006
Посилання
- Екстремум функції двох змінних // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 353. — 594 с.
- Gray, Lawrence F.; Flanigan, Francis J.; Kazdan, Jerry L.; Frank, David H.; Fristedt, Bert (1990). Calculus two: linear and nonlinear functions. Berlin: Springer-Verlag. с. 375. ISBN 0-387-97388-5.
- Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (вид. 2nd). New York, NY: Chelsea. ISBN 978-0-8284-1087-8.
- von Petersdorff, Tobias (2006). Critical Points of Autonomous Systems. Differential Equations for Scientists and Engineers (Math 246 lecture notes).
- Widder, D. V. (1989). Advanced calculus. New York, NY: Dover Publications. с. 128. ISBN 0-486-66103-2.
- Agarwal, A. Study on the Nash Equilibrium (Lecture Notes).