Управління товарними запасами

(модель із постійним контролем, модель із оперативною інформацією)

У моделі з фіксованим обсягом партії замовлення здійснюється щоразу, коли запас у системі опускається до певного рівня.

Основні моделі оперативного керування запасами такі:

• <Q, r>-модель: при зниженні запасів до рівня r замовляється партія розміром Q (малюнок 1).
• <R, r>-модель: якщо рівень запасів знижується до ${\displaystyle x\leq r}$, при надходженні однієї з вимог, то робиться замовлення розміром ${\displaystyle (R-x)}$.

Мал. 1. <Q, r>-модель керування запасами при випадковому попиті

(модель із періодичними перевірками)

У системах з періодичною перевіркою періодом функціонування T уважається інтервал між двома послідовними перевірками. Замовлення на поповнення запасу подається в момент перевірки, якщо попит за попередній період функціонування відмінний від нуля.

Розглядаються такі моделі керування запасами при періодичних перевірках:

• <R, T>-модель, заснована на R-стратегії: у момент перевірки замовляється партія, що доводить фіктивних рівень запасів (тобто сума наявного запасу та замовленого) до рівня R;
• <R, r, T>-модель, заснована на Rr-стратегії: замовлення на поповнення запасу до рівня R подається, якщо в момент перевірки фіктивний рівень запасів у системі менше або дорівнює r;
• <n, r, T>-модель, заснована на nQ-стратегії: замовлення на поповнення запасу подається, якщо в момент перевірки фіктивний рівень запасів у системі менше або дорівнює r. Обсяг партії замовлення кратний деякій фіксованій величині Q, n — найбільше ціле число, для якого фіктивний рівень запасів після подачі замовлення виявляється меншим або рівним ${\displaystyle R=r+Q}$.

Основним параметром системи керування товарними запасами є попит. У реальності попит, найчастіше, має випадковий характер. Використання моделей керування запасами, для яких попит — відома величина, обмежено.

Залежно від характеру товару й ступеня лояльності споживача можна виділити два типи реакції покупця на дефіцит. У першому випадку незадоволені вимоги стають на облік, тобто покупець погоджується почекати поставки товару (малюнок 2). У другому випадку незадоволені вимоги губляться, тобто покупець задовольняє потребу у відсутньому товарі з іншого джерела (малюнок 3).

Мал. 2 — Рівень запасу в системі з урахуванням незадоволених вимог

На даному малюнку s — число вимог, зареєстрованих до моменту поставки, T1 — час протягом якого надійдуть вимоги на (Q — s) одиниць, а Т2 — час, коли вимоги стають на облік.

Середні річні витрати (TCU) і оптимальний розмір замовлення (Q*) визначаються за такими формулами:

${\displaystyle TCU(Q)={\frac {\lambda }{Q}}\cdot K+{\frac {h}{2Q}}(Q-s)^{2}+{\frac {Ps^{2}}{2Q}}}$

${\displaystyle Q^{*}={\sqrt {\frac {2\lambda K}{h}}}\cdot {\sqrt {\frac {P+h}{P}}}}$

де ${\displaystyle \lambda }$ — інтенсивність попиту.

Графічно поводження системи із втратою незадоволених вимог представлено на малюнку 3.

Мал. 3 — Рівень запасу в системі із втратою незадоволених вимог

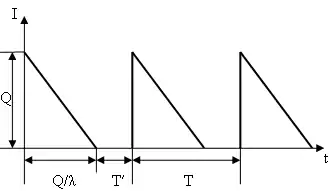
На малюнку T' — час, протягом якого незадоволені вимоги губляться.

Середні витрати й оптимальний розмір замовлення визначаються за формулами:

${\displaystyle TCU(Q)={\frac {\lambda K}{Q+\lambda T'}}+{\frac {h}{2}}\cdot {\frac {Q^{2}}{Q+\lambda T'}}+{\frac {G\lambda }{Q+\lambda T'}}\cdot \lambda T'}$

${\displaystyle Q^{*}={\sqrt {{\frac {2\lambda K}{h}}\cdot {\frac {G}{h+G}}}}}$

Часто в системах керування запасами передбачається що частина запасу губиться, а частина — ураховується. Для цього вводиться коефіцієнт ${\displaystyle \beta }$ — частка незадоволеного попиту, що може бути врахована.

Знижка на розмір замовлення буває двох видів:

• «оптова» знижка;
• диференціальна знижка.

«Оптова» знижки поширюється на кожну одиницю закуповуваного товару залежно від загального обсягу партії. Для системи з «оптовою» знижкою при розмірі закупівлі рівному ${\displaystyle Q,q_{i}\leq Q<q_{i+1}}$, ціна товару для кожної одиниці партії дорівнює ${\displaystyle C_{i}}$, причому ${\displaystyle C_{i+1}<C_{i}}$.

Середні річні витрати визначаються як:

${\displaystyle TCU_{i}(Q)={\frac {\lambda K}{Q}}+{\frac {h\cdot Q}{2}}+\lambda C_{i},\qquad q_{i}\leq Q<q_{i+1}}$

Графічно середні річні витрати представлені на малюнку 4.

Мал. 4 — Середні річні витрати при оптовій знижці

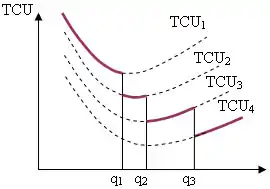
Для визначення оптимального розміру партії використається наступний алгоритм:

1. Обчислюється ${\displaystyle Q_{n}}$. Якщо ${\displaystyle Q_{n}\geq \ q_{n-1}}$, то ${\displaystyle Q_{n}}$ — оптимально.
2. Якщо ${\displaystyle Q_{n}<q_{n-1}}$, то обчислюється ${\displaystyle Q_{n-1}}$. Якщо ${\displaystyle Q_{n-1}\geq \ q_{n-2}}$, то ${\displaystyle TCU(Q_{n-1})}$ порівнюється з ${\displaystyle TCU(q_{n-1})}$, і мінімум з них відповідає оптимальному розміру замовлення.
3. Якщо ${\displaystyle Q_{n-1}<q_{n-2}}$, то обчислюється ${\displaystyle Q_{n-2}}$. Якщо ${\displaystyle Q_{n-2}\geq \ q_{n-3}}$, то ${\displaystyle TCU(Q_{n-2})}$ порівнюється з ${\displaystyle TCU(q_{n-3})}$ і ${\displaystyle TCU(q_{n-1})}$, і мінімум з них відповідає оптимальному розміру замовлення.
4. Обчислення тривають доти, поки не відшукується мінімум. Потрібно не більше n кроків.

Диференціальна знижка поширюється на кожну наступну одиницю закуповуваного товару, що перевищує певний обсяг замовлення.

Диференціальна знижка полягає в тому, що якщо розмір замовлення коливається від 1 до ${\displaystyle q_{1}}$, то вартість одиниці виробу складе ${\displaystyle c_{0}}$, при розмірі замовлення від ${\displaystyle q_{1}+1}$ до ${\displaystyle q_{2}}$ вартість складе ${\displaystyle c_{0}}$ для ${\displaystyle q_{1}}$ одиниць товару й ${\displaystyle c_{1}}$ для ${\displaystyle (Q-q_{1})}$ одиниць товару й т.  д.

Середні річні витрати при ${\displaystyle q_{i}<Q\leq \ q_{i+1}}$ визначаються за наступною формулою:

${\displaystyle TCU_{i}=\lambda \cdot C_{i}+{\frac {\lambda }{Q}}\left(K+R_{i}-C_{i}q_{i}\right)+{\frac {IR_{i}}{2}}+h\left({\frac {Q-q_{i}}{2}}\right),\qquad i=[0,m]}$

де ${\displaystyle R_{i}}$ — витрати на закупівлю ${\displaystyle q_{i}}$ одиниць виробу, ${\displaystyle R_{0}=0,q_{0}=0,q_{m+1}=\propto }$.

${\displaystyle C(Q)=R_{i}+C_{i}(Q-q_{i}),\qquad i=[0,m]}$.

Графік середніх річних витрат зображений на малюнку 5.

Мал. 5 — Середні річні витрати при диференціальній знижці

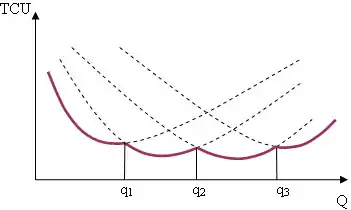
Для обчислення Q оптимального використається наступний алгоритм:

1. обчислюються значення ${\displaystyle Q^{(i)}}$: ${\displaystyle Q^{(i)}={\sqrt {\frac {2\lambda (K+R_{i}-c_{i}q_{i})}{h}}}}$
2. для значень ${\displaystyle Q^{(i)}}$, що задовольняють умові ${\displaystyle q_{i}<Q^{(i)}\leq q_{i+1}}$ визначається значення ${\displaystyle TCU(Q^{(i)})}$.
3. Оптимальним буде ${\displaystyle Q^{(i)}}$, що відповідає мінімальним витратам.

Обмежений строк зберігання товару характерний для більшості товарів роздрібної торгівлі. Це можуть бути товари які поступово, за час зберігання гублять свої споживчі якості (наприклад фрукти), так і товари, які не будучи реалізованими за певний строк повністю втратять споживчі якості (наприклад газети).

Управління запасами товарів з обмеженим строком придатності відбувається в такий спосіб:

1. визначається оптимальний розмір замовлення (з урахуванням витрат на зберігання, на дефіцит і списання застарілих товарів) і подається замовлення на поповнення запасу;
2. весь прибулий продукт уважається новим;
3. відпускання товару провадиться за принципом «перший прийшов — перший вийшов (пішов)» (FIFO та LIFO);
4. продукт, не реалізований протягом строку зберігання, m, списується.

Для точного опису наявного запасу в кожен момент часу й рівня запасів у системі (U) використовуються такі формули:

${\displaystyle {\begin{cases}x_{mt}=(Q_{t})^{+}\\\left(x_{i+1,t-1}-\left[d-\sum _{j=1}^{i}x_{j,t-1}\right]^{+}\right)^{+},\qquad i=[1,m-1]\end{cases}}}$

${\displaystyle U_{t}=\sum _{i=1}^{m}x_{i,t}}$

де ${\displaystyle x_{i,t}}$ — кількість запасів на момент часу t зі строком зберігання, що залишився, рівним i;

m — строк придатності продукту;

d — попит на товар;

${\displaystyle (a)^{+}=max(0,a)}$.

Тоді, для системи керування запасами з постійним контролем можна вивести співвідношення, що дозволяє визначити середні витрати в одиницю часу i:

${\displaystyle TCU(i)={\frac {d_{i}}{Q}}K+C\cdot d_{i}+B\cdot \beta (d_{i}-U_{i})^{+}+G(1-\beta )(d_{i}-U_{i})^{+}+W(x_{1,i}-d_{i})^{+}+h(U_{i}-d_{i})^{+}}$

де ${\displaystyle d_{i}}$ — попит на товар за час i.

При взаємодії декількох товарів у системі виникають такі задачі управління запасами:

• задача сполучення замовлень за декількома номенклатура ми (загальний постачальник);
• багатономенклатурні задачі управління запасами із взаємозамінними продуктами;
• багатономенклатурні задачі управління запасами з обмеженнями (на площу склада, на кількість капіталовкладень у формування запасів, на загальне число замовлень).