Формули Мольвейде

Формули Мольвейде — тригонометричні залежності, що виражають відношення між довжинами сторін і значеннями кутів при вершинах деякого трикутника, відкриті К. Б. Мольвейде.

Трикутник на площині.

Опис

Формули Мольвейде виглядають так:

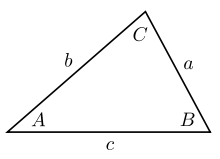
{\frac {a+b}{c}}={\frac {\operatorname {cos} \;{\frac {A-B}{2}}}{\operatorname {sin} \;{\frac {C}{2}}}};

{\frac {a-b}{c}}={\frac {\operatorname {sin} \;{\frac {A-B}{2}}}{\operatorname {cos} \;{\frac {C}{2}}}},

де A, B, C — значення кутів при відповідних вершинах трикутника і a, b, c — довжини сторін, відповідно між вершинами B і C, C і A, A і B. Формули названо на честь німецького математика Карла Мольвейде. Формули Мольвейде зручно використовувати при розв'язуванні трикутника за двома сторонами і кутом між ними[1]^:146 і за двома кутами і прилеглою до них стороною. Аналогічні співвідношення у сферичній тригонометрії називають формулами Деламбра^:83.

Доведення

Розглянемо виведення тільки першого співвідношення, оскільки друге доводиться аналогічно.

{\frac {a+b}{c}}={\frac {\operatorname {cos} \;{\frac {A-B}{2}}}{\operatorname {sin} \;{\frac {C}{2}}}};

З теореми синусів:

{\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}

маємо:

{\frac {a}{c}}={\frac {\sin A}{\sin C}}

{\frac {b}{c}}={\frac {\sin B}{\sin C}}

звідки випливає:

{\frac {a+b}{c}}={\frac {\sin A+\sin B}{\sin C}}

Враховуючи формули подвійного кута для синуса:

\sin C=2\sin {\frac {C}{2}}\cos {\frac {C}{2}}

,

а також формули для суми синусів:

\sin A+\sin B=2\sin {\frac {A+B}{2}}\cos {\frac {A-B}{2}}

маємо:

{\frac {a+b}{c}}={\frac {\sin A+\sin B}{\sin C}}={\frac {\sin {\frac {A+B}{2}}\cos {\frac {A-B}{2}}}{\sin {\frac {C}{2}}\cos {\frac {C}{2}}}}

За теоремою про суму кутів трикутника:

C=\pi -(A+B)

звідки, з урахуванням формул зведення для косинуса випливає, що:

\cos {\frac {C}{2}}=\cos {\frac {\pi -(A+B)}{2}}=\sin {\frac {A+B}{2}}

як наслідок, маємо:

{\frac {a+b}{c}}={\frac {\cos {\frac {A-B}{2}}}{\sin {\frac {C}{2}}}}

що й потрібно було довести.

Застосування

Поділивши окремо праві й ліві частини останніх формул, відразу отримаємо теорему тангенсів

Див. також

Примітка

Степанов Н. Н. Сферическая тригонометрия. — М. — Л. : ОГИЗ, 1948. — 154 с.

Література

О. В. Мантуров, Ю. К. Солнцев, Ю. И. Соркин, Н. Г. Федин. Толковый словарь математических терминов, М.: Просвещение, 1965.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[St-1] Степанов Н. Н. Сферическая тригонометрия. — М. — Л. : ОГИЗ, 1948. — 154 с.