Список тригонометричних тотожностей
Тригонометричні тотожності — математичні вирази з тригонометричними функціями, що виконуються для всіх значень аргумента зі спільної області визначення.
| Тригонометрія |
|---|
 |
|
| Посилання |
|
| Закони і теореми |
| Обчислення |
|
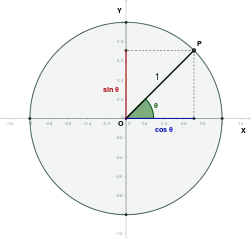
Основні позначення
Кути
В цій статті кути позначені грецькими буквами і т. д. Величину кута найчастіше задають в градусах або радіанах:
- 1 повне коло = 360 градусів = 2 радіан
В наступній таблиці наведено спвівідношення між значеннями в градусах і радіанах для деяких кутів
| Градуси | 30° | 60° | 120° | 150° | 210° | 240° | 300° | 330° |
|---|---|---|---|---|---|---|---|---|
| Радіани | ||||||||
| Градуси | 45° | 90° | 135° | 180° | 225° | 270° | 315° | 360° |
| Радіани | ||||||||
Якщо не сказано інакше, то всі кути задано у радіанах, а кути, що закінчуються символом (°) — в градусах.
Тригонометричні функції
У статті будуть наведені співвідношення та тотожності для шести основних тригонометричних функцій:
- синус
- косинус
- тангенс
- котангенс
- секанс
- косеканс
В англомовній літературі тангенс та котангенс зазвичай позначають та відповідно.
Обернені тригонометричні функції
Обернені тригонометричні функції це такі функції, композиція яких зі звичайними тригонометричними функціями дає тотожне відображення. Наприклад, функція обернена до синуса, відома як обернений синус (sin−1) або арксинус (arcsin or asin), задовольняє співвідношення
та
Тригонометричні функції та обернені до них наведені в наступній таблиці:
| Функція | sin | cos | tg | ctg | sec | csc |
|---|---|---|---|---|---|---|
| Обернена | arcsin | arccos | arctg | arcctg | arcsec | arccsc |
Екзотичні тригонометричні функції
Крім основних шести, також використовують інші тригонометричні функції кута. Їх використовували раніше при розв'язуванні різних навігаційних задач, однак з розвитком обчислювальної техніки вони втратили свою актуальність.
| Назва | Скорочене позн. | Значення |
|---|---|---|
| синус-верзус | ||
| косинус-верзус | ||
| коверсинус | ||
| коверкосинус | ||
| гаверсинус | ||
| гаверкосинус | ||
| когаверсинус | ||
| когаверкосинус | ||
| ексеканс | ||
| екскосеканс | ||
| хорда |
Таблиці значень тригонометричних функцій
В тих точках, де значення тангенса та котангенса прямують до нескінченності знак залежить від того з якого боку до цієї точки ми підходимо.
Для тангенса — якщо справа, то , а якщо зліва, то . Для котангенса навпаки.
Основні тригонометричні формули
| Основні формули | |
|---|---|
| (1) | |
| (2) | |
| (3) | |
Формула (1) є наслідком теореми Піфагора (Тригонометрична тотожність Піфагора). Формули (2) і (3) добуваються діленням формули (1) на та відповідно.
Співвідношення між основними тригонометричними функціями
Формули зведення
Сукупність формул, що відображають симетрію тригонометричних функцій відносно певних значень кутів, перетворення при зсуві аргументу на деякий кут, а також періодичність тригонометричних функцій.
Симетрія
Виконуються такі співвідношення:
| Симетрія відносно кута | Симетрія відносно (співвідношення між ко-функціями) |
Симетрія відносно |
|---|---|---|
Зсув та періодичність
Співвідношення часто використовують для спрощення обчислень.
| Зсув на π/2 | Зсув на π Період tg і ctg |
Зсув на 2π Період sin, cos, csc і sec |
|---|---|---|
Формули для суми аргументів
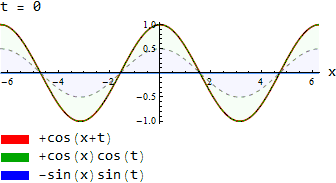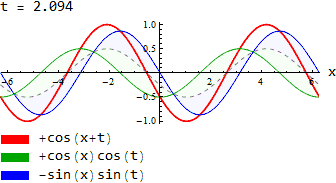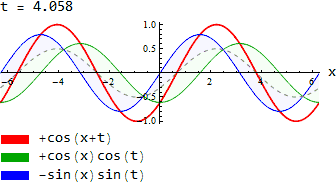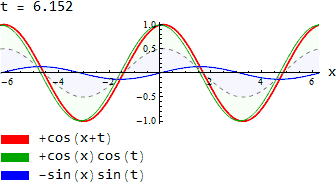
| Формули для суми аргументів | |
|---|---|
| (5) | |
| (6) | |
| (7) | |
Формула (7) отримана діленням (5) на (6).
Синус і косинус від нескінченної суми
У правих частинах рівності суму взято по всіх підмножинах натуральних чисел з 2k+1 або 2k елементів відповідно.
Тангенси від сум аргументів
Нехай — елементарні симетричні многочлени степеня k від n змінних
Наприклад:
Тоді
Наприклад:
і так далі.
Секанс і косеканс від суми аргументів
де ek — елементарні симетричні многочлени степеня k від n змінних (дивись пункт тангенси від сум аргументів)
Наприклад,
Формули подвійного кута
Формули подвійного кута виведені з формул (5), (6) і (7), якщо взяти кут β рівним α:
| Формули подвійного кута | |
|---|---|
| (23) | |
| (24) | |
| (25) | |
Формули потрійного кута
| Формули потрійного кута |
|---|
Формули кратних кутів
| Формули кратних кутів |
|---|
де — ціла частина числа , — біноміальний коефіцієнт.
Формули для кратних кутів виводяться за допомогою формули Муавра
Розкриємо праву частину рівності за формулою бінома Ньютона
Врахувавши, що та виділивши окремо дійсну та уявну частини, рівність запишемо у вигляді
Підставимо отриману рівність у формулу Муавра
Оскільки два комплексні числа рівні тоді і лише тоді коли рівні їхні дійсні та уявні частини, то з останньої рівності отримуємо шукані формули
Ітераційні формули
З використанням спеціальних многочленів
Мають місце такі співвідношення:
де — поліном Чебишова першого роду степеня n.
Зображення у вигляді скінченних добутків
Формули половинного кута
| Формули половинного кута |
|---|
Знак перед виразом обрано відповідно до того, до якого квадранту належить кут .
Формули пониження степеня
Формули пониження степеня виведені з формул подвійного кута:
| Синус | Косинус | Інше |
|---|---|---|
Формули перетворення добутків функцій
| Формули перетворення добутків функцій | |
|---|---|
| (28) | |
| (29) | |
| (30) | |
| (31) | |
| (32) | |
| (33) | |
| (34) | |
Формули перетворення суми функцій
| Формули перетворення суми функцій | |
|---|---|
| (35) | |
| (36) | |
| (37) | |
| (38) | |
| (39) | |
| (40) | |
| (41) | |
| (42) | |
| (43) | |
| (43) | |
Загальні суми
Якщо ж таке, що , то при отримуємо
Ядро Діріхле та ядро Феєра
Сума виду
називається ядром Діріхле.
А функція
називається ядром Феєра
- ,
Вони використані при сумуванні рядів Фур'є.
Зображення через нескінченні добутки
Співвдношення за додаткових обмежень на значення кутів
- Нехай
тоді
Зауважимо, що наведені вище співвідношення справджуються, якщо — кути деякого трикутника.
- Нехай
тоді
- Нехай
тоді
Обернені тригонометричні функції
Поєднання тригонометричних та обернених їм функцій
| Поєднання тригонометричних та обернених їм функцій | |
|---|---|
Додавання обернених тригонометричних функцій
Нехай такі, що , тоді
Розв'язок найпростіших тригонометричних рівнянь
- .
- Якщо — дійсних розв'язків не існує.
- Якщо — роз'язком є число виду .
- .
- Якщо — розв'язків нема.
- Якщо — роз'язком є число виду .
- .
- Розв'язком є число виду .
- .
- Розв'язком є число виду .
Розв'язок найпростіших тригонометричних нерівностей
| Вид нерівності | Множина розв'язків, |
|---|---|
Одна корисна нерівність
Для довільного з інтервалу виконуються такі нерівності:
Універсальна тригонометрична підстановка
Тотожності мають зміст лише тоді, коли існують обидві частини (тобто при ).
Допоміжний аргумент (метод Юніса)
Перші дві формули можуть бути узагальненими
де
Зв'язок з комплексною екпонентою
Експоненційне зображення тригонометричних функцій та обернених їм
| Функція | Обернена функція |
|---|---|
Числові співвідношення
Різне
Див. також
Література
- Абрамовиц М., Стиган И. Справочник по специальным функциям. — Москва : Наука, 1979. — 832 с.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. — Москва : Физматгиз, 1963. — 1100 с.
