Фотометричний парадокс
Фотометри́чний парадо́кс або парадо́кс Шезо́—О́льберса — суперечність між яскравістю нічного неба, що спостерігається, та теоретичною його яскравістю в моделі статичного нескінченного Всесвіту, досить рівномірно заповненого зорями[1].
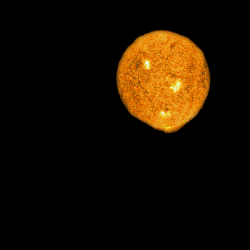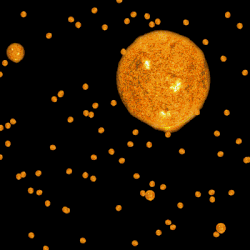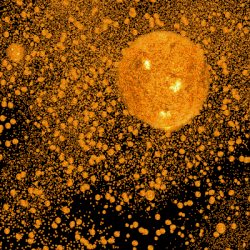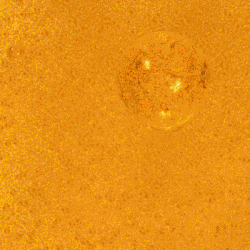
Опис проблеми
На думку більшості астрономів XVIII і XIX століття космологічна картина Всесвіту була досить простою: Всесвіт вважали нескінченим, вічним, простір — евклідовим, зорі — більш-менш стабільними, а світність одиниці об'єму — сталою.
Швейцарський астроном Жан Філіп де Шезо (1744 р.) і незалежно від нього[джерело?] Генріх Ольберс (1826 р.) звернули увагу на суперечність такої космологічної картини із найдавнішим астрономічним спостереженням — що небо темніє після заходу Сонця.
Справді, в наївній космологічній моделі освітленість від зорі з абсолютною світністю , віддаленої на відстань , дорівнюватиме (нехтуючи поглинанням світла).
Якщо густина таких зір у Всесвіті постійна, то кількість зір, віддалених на відстань між і , дорівнює: а густина загальної випроміненої енергії всіх зір дорівнює
Цей інтеграл розбіжний, тобто, густина енергії зоряного світла нескінченна.
Фізична сутність парадоксу
У нескінченному Всесвіті, який із постійною щільністю заповнено зорями, будь-який промінь зору має закінчуватися зорею, аналогічно до того, як у густому лісі ми виявляємо себе оточеними «стіною» з віддалених дерев[2]. Потік енергії випромінювання, що сприймається від зорі, зменшується обернено пропорційно квадрату відстані до неї. Але кутова площа (тілесний кут), охоплений на небі кожною зорею, також зменшується обернено пропорційно квадрату відстані, з чого випливає, що поверхнева яскравість зорі (що дорівнює відношенню потоку енергії до тілесного кута, який займає на небі зоря) не залежить від відстані (так само як однаково яскравими виявляються близькі та віддалені дерева). Оскільки наше Сонце є типовою зорею, то поверхнева яскравість будь-якої зорі в середньому має дорівнювати поверхневій яскравості Сонця. Це значить, що коли ми дивимося в будь-яку точку неба, ми повинні бачити зорю з тією ж поверхневою яскравістю, що й Сонце; поверхнева яскравість сусідньої точки має бути такою ж, і взагалі в усіх точках неба поверхнева яскравість має бути рівною поверхневій яскравості Сонця, оскільки в будь-якій точці небосхилу перебуватиме якась зоря. Отже, все небо (не лише вночі, але й удень) має бути так само яскравим, як поверхня Сонця.
Вперше цей парадокс повністю сформулював швейцарський астроном Жан Філіп Луї де Шезо (1718—1751) 1744 р., хоча аналогічні думки висловлювали раніше й інші вчені, зокрема, Йоганн Кеплер, Отто фон Геріке і Едмунд Галлей. Іноді фотометричний парадокс називають парадоксом Ольберса, на честь астронома, який привернув до нього увагу в XIX сторіччі.
Вирішення
У минулому робилися спроби вирішити цей парадокс припущенням, що хмари космічного пилу екранують світло далеких зір. Але це пояснення некоректне: в однорідному ізотропному Всесвіті пил має нагріватися й світитися так само яскраво, як і зорі. Інше пояснення полягало в тому, що нескінченний Всесвіт влаштований ієрархічно, подібно матрьошці: кожна система входить до складу системи вищого рівня, так що середня щільність випромінювачів світла у міру зростання масштабів прямує до нуля. Однак це припущення відкидається в сучасній космології, заснованій на космологічному принципі, згідно з яким Всесвіт на великих масштабах однорідний (та ізотропний).
Правильне пояснення фотометричного парадокса міститься в космологічній поемі «Еврика» відомого американського письменника Едгара По (1848 р.); оскільки ця поема не є науковим твором, авторство може належати також німецькому астроному Йоганну Медлеру (1861 р.) Детальний математичний розгляд цього питання був поданий Вільямом Томсоном (лордом Кельвіном) й 1901 р. Він заснований на твердженні про скінченність часу існування Всесвіту. Оскільки (за сучасними даними) понад 13 млрд років тому у Всесвіті не було галактик і квазарів, найвіддаленіші зорі, які ми можемо спостерігати, розташовані на відстанях близько 13 млрд св. років. Це усуває основну передумову фотометричного парадокса — що зорі розташовані на будь-яких, як завгодно великих відстанях від нас. Всесвіт, що спостерігається на великих відстанях, настільки молодий, що зорі ще не встигли в ньому утворитися. Це анітрохи не суперечить космологічному принципу, з якого випливає безмежність Всесвіту: обмежений не Всесвіт, а лише та його частина, де за час приходу до нас світла встигли народитися перші зорі.
Деякий (істотно менший[відсутнє в джерелі]) внесок у зменшення яскравості нічного неба вносить і червоний зсув галактик. Справді, спостережуване випромінювання далеких галактик має в (1+z) більшу довжину хвилі, ніж галактик на близьких відстанях. Але довжина хвилі пов'язана з енергією світла за формулою ε = hc / λ. Тому енергія фотонів, що надходять до нас від далеких галактик, в (1+z) разів менша. Далі, якщо з галактики із червоним зсувом z вилітають два фотони з інтервалом часу δt, то інтервал між надходженням цих двох фотонів на Землі буде ще в (1+z) разів більшим, отже, інтенсивність прийнятого світла в стільки ж разів буде меншою. У результаті ми отримуємо, що сумарна енергія, яка надходить до спостерігача від далеких галактик, в (1+z)² разів менша, ніж у випадку, коли галактики не віддаляються внаслідок космологічного розширення[1].
Таким чином, фотометричний парадокс наявний лише в наївній моделі статичного нескінченного Всесвіту і легко усувається в сучасних моделях Всесвіту, який розширюється[1].
Джерела
- Фотометричний парадокс // Астрономічний енциклопедичний словник / за заг. ред. І. А. Климишина та А. О. Корсунь. — Львів : Голов. астроном. обсерваторія НАН України : Львів. нац. ун-т ім. Івана Франка, 2003. — С. 500. — ISBN 966-613-263-X.
- ВЧЕНІ ПОЯСНИЛИ, ЧОМУ НІЧНЕ НЕБО ТЕМНЕ
Література
- Steven Weinberg,MIT, «Gravitation and Cosmolgy»
- The Dark Night Sky Riddle - Olber's Paradox
- Gravity and Light in the Newtonian Universe of Stars
- J.M. Overduin a and P.S. Wesson. Dark Matter and Background Light
- Tipler, F. J. (1988). Johann Madler's Resolution of Olber's Paradox. Quarterly Journal of the Royal Astronomical Society 29 (3/SEP): 313. Bibcode:1988QJRAS..29..313T.
- The extra-galactic background light: A modern version of Olbers' paradox
