Фільтр низьких частот
Фі́льтр ни́зьких часто́т (англ. low-pass filter) — фільтр, який пропускає низькі частоти, та послаблює частоти, розташовані вище частоти зрізу фільтру (англ. cutoff frequency)[1].
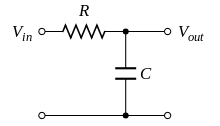
RC фільтр
На малюнку праворуч зображена схема фільтру на основі RC-ланцюга, який відсікає високочастотні коливання. Реактивний опір конденсатора зменшується з частотою, а отже конденсатор пропускає тільки високочастотні сигнали, й тим краще, чим вища частота. У результаті на високих частотах конденсатор шунтує сигнал. На виході такого чотириполюсника залишиться лише сигнал низької частоти.
Характерна частота RC фільтру:
- .
Характеристики
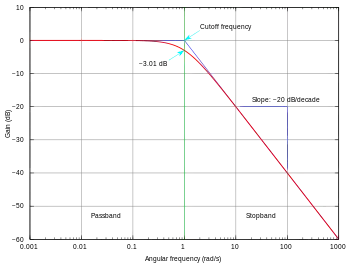
Крутизна зрізу (англ. slope) (вимірюється у дБ/декада або дБ/октава) визначає зміну характеристики фільтра при переході від області пропускання до області редукції.
Реалізація для дискретного часу
Існує багато цифрових фільтрів, які розроблені так, щоб повторювати характеристики фільтрів низьких частот. Широко використовуються як, рекурсивні фільтри так і фільтри із скінченною імпульсною характеристикою, а також фільтри із застосуванням перетворення Фур'є.
Простий рекурсивний фільтр
Ефект рекурсивного фільтру низьких частот можна повторити на комп'ютері якщо проаналізувати поведінку RC фільтру в часовій області і після того дискретизвувати модель.
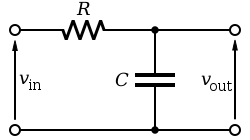
Із діаграми електричного кола, що праворуч, відповідно до Законів Кірхгофа і визначення ємності маємо:
()
()
()
де це заряд, що накопичується на ємності у момент часу . Підстановка рівняння Q у рівняння I дасть , що в свою чергу можна підставити в рівняння V, таким чином:
Це рівняння можна дискретизувати. Для простоти, припустимо що інтервали часу входу і виходу розподілені рівномірно в часі і мають довжину . Нехай інтервали для задаються послідовністю , а інтервали задаються послідовністю , що відповідають однаковим точкам у часі. Виконавши ці підстановки:
І перевпорядкувавши ці терми, отримаємо рекурентне співвідношення
Це реалізація у дискретному часі простого RC фільтра низьких частот із експоненційно згладженим рухомим середнім
За визначенням, коефіцієнт згладжування . Вираз для дозволяє отримати еквівалент для дискретного часту для сталого періоду і коефіцієнта згладжування :
Пригадавши, що
- звідси
тоді і співвідносяться як:
і
- .
Якщо , стала дорівнює довжині інтервалів. Якщо , тоді набагато більша за інтервал, і .
Рекурсивне рівняння для фільтра дозволяє розрахувати вихідні значення за даними інтервалами на основі вхідних значень і значення виходу на попередньому інтервалі. Наступний алгоритм на псевдокоді алгоритм моделює роботу фільтру низьких частот на послідовності цифрових даних:
// Return RC low-pass filter output samples, given input samples, // time interval dt, and time constant RC function lowpass(real[0..n] x, real dt, real RC) var real[0..n] y var real α := dt / (RC + dt) y[0] := α * x[0] for i from 1 to n y[i] := α * x[i] + (1-α) * y[i-1] return y
Цикл, який підраховує кожний результат для n можна спростити у його еквівалент:
for i from 1 to n
y[i] := y[i-1] + α * (x[i] - y[i-1])
Це означає, що зміна одного вихідного відліку фільтру до значення наступного відліку пропорційна різниці між попереднім результатом і наступним входом.
Посилання
- Хоровиц П., Хилл У. Искусство схемотехники (в 2-х томах) = The Art of Electronics. — М.: Мир, 1980. — Т. 2. — 590 с. (рос.)