Число закрученості

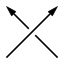
В теорії вузлів, число закрученості будується за діаграмою орієнтованого зачеплення. Воно дорівнює різниці між числом додатних і від'ємних перехресть (див. мал. нижче). Іншими словами - ми обходимо в заданих напрямках усі компоненти зачеплення, і кожен раз, коли проходимо через перехрестя зверху, додаємо +1, якщо компонента, що йде знизу, перетинає наш шлях справа наліво, і -1, якщо зліва направо.

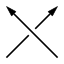Додатне перехрестя		Від'ємне перехрестя

Для діаграми вузла, число закрученості (і просто типи перехресть) не змінюються під час зміни орієнтації, тому число закрученості коректно визначено і для неорієнтованої діаграми.

Число закрученості інваріантне відносно рухів Рейдемейстера II і III типів. Навпаки, рух Рейдемейстера I типу збільшує або зменшує число закрученості на 1, тому воно не є інваріантом ізотопії вузла, а тільки функцією від діаграми.

У разі, якщо діаграма зображує тривіальний вузол, число закрученості - це число оборотів, на які виявиться закрученим пас, якщо його пустити вздовж цієї діаграми (так, щоб він щільно прилягав до площини), а потім, не розриваючи, розпрямити вздовж кола (з закрученням у той чи інший бік).