Ядрова оцінка густини розподілу
В статистиці, я́дрова оці́нка густини́ розпо́ділу (англ. Kernel density estimation) — це непараметричний метод оцінки функції густини випадкової величини за вибіркою. Ядрова оцінка густини є важливою задачею згладжування даних; при застосуванні методу судження щодо статистичних властивостей популяції здійснюється на базі скінченної вибірки. В деяких галузях (таких як обробка сигналів, економетрика) поряд з ядровою оцінкою густини використовують назву вікно Парцель-Розенблата, на честь Емануеля Парцена та Мюрея Розенблата, котрі незалежно один від одного створили метод в теперішньому його вигляді.[1][2]
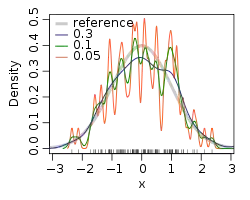
Визначення
Нехай (x1, x2, …, xn) — вибірка н.о.р.в.в., отримана з деякого розподілу з невідомою густиною ƒ. Потрібно оцінити форму цієї функції ƒ. Ядрова оцінка цієї густини ƒ задається формулою
де K(·) — статистичне ядро — симетрична, але не обов'язково додатня функція з інтегралом рівним одиниці, h > 0 — параметр згладжування, який ще називають пропускно́ю зда́тністю.
Практичне обчислення параметру згладжування
Якщо використовується гаусівські ядрові функції для оцінки одновимірних даних і оцінювана базова густина є стандартною нормальною, тоді можна показати, що оптимальним значенням параметру згладжування, h, є
- , де — стандартне відхилення вибірки, що оцінюється.
Таке наближення називається нормально розподілене наближення (або гаусівське наближення).
Джерела
- Rosenblatt, M. (1956). Remarks on some nonparametric estimates of a density function. Annals of Mathematical Statistics 27: 832–837. doi:10.1214/aoms/1177728190. (англ.)
- Parzen, E. (1962). On estimation of a probability density function and mode. Annals of Mathematical Statistics 33: 1065–1076. doi:10.1214/aoms/1177704472. (англ.)