Ядро (статистика)
Ядро або ядрова функція — це вагова функція, що використовується в непараметричних методах оцінки. Ядра використовуються при ядерній оцінці щільності розподілу для оцінки густини випадкової величини, чи в ядерній регресії для оцінки умовного математичного сподівання випадкової величини. Ядра також використовуються в часових рядах як переіодограми для оцінки спектральної щільності. Додаткового використання ядра набули в оцінці інтенсивності точкового процесу зміної в часі.
Визначення
Ядром називається невід'ємна дійснозначна інтегровна функція K, яка задовольняє дві наступні властивості:
Перша умова гарантує, що метод ядерної оцінки щільності розподілу дійсно дає густину випадкової величини. Друга — гарантує, що середнє значення знайденого розподілу дорівнює середньому значенню вибірки для якої оцінюють густину.
Якщо K — ядро, тоді функція K* визначена таким чином K*(u) = λ−1K(λ−1u), де λ > 0 також є ядерною функцією. Цю властивість можна використати для вибору масштабу максимально узгодженого з даними.
Використання ядер
Звичайно використовують кілька видів ядрових функцій: рівномірну, трикутну, Епанечнікова, Четвертинну (двоточкову), кубічну (триточкову), Гауса та косинусну.
В таблиці нижче, 1{…} — характеристична функція.
| Ядрові функції, K(u) | ||||
|---|---|---|---|---|
| Рівномірна | 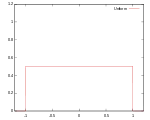 |
|||
| Трикутна | 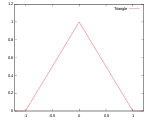 |
|||
| Епанечнікова | 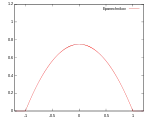 |
|||
| Четвертинна (двоточкова) |
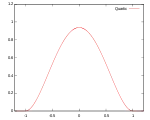 |
|||
| Кубічна (триточкова) |
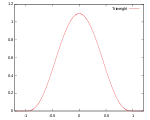 |
|||
| Гауса | 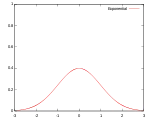 |
|||
| Косинус | 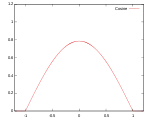 |
|||
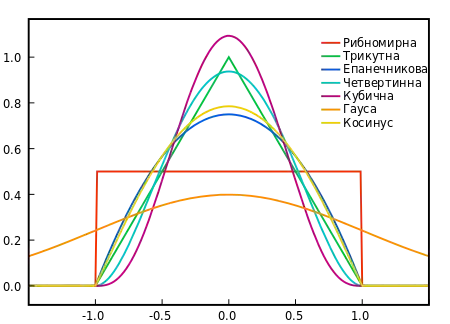
Джерела
- Li, Qi; Racine, Jeffrey S. (2007). Nonparametric Econometrics: Theory and Practice. Princeton University Press. ISBN 0691121613.
Посилання
- Kernel Basis function (англ.) (з малюнками).