Ґратка Бете

Ґратка Бете, або дерево Келі (різновид графу Келі) — безмежний зв'язаний граф без циклів (дерево), кожен вузол якого сполучений з z сусідами. Число z називають координаційним числом. Це дерево з коренем, оточеним послідовністю оболонок. Число вершин у k-ій оболонці дорівнює:

\,N_{k}=z(z-1)^{k-1}.

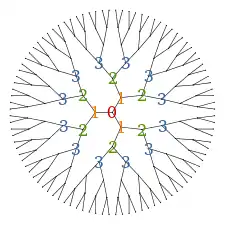
Ґратка Бете з координаційним числом z = 3

Таку ґратку запропонував 1935 року[1] Ганс Бете. Завдяки її простоті багато задач статистичної механіки на цій структурі можна розв'язати точно[2].

Виноски

Bethe, H. A. (1935). Statistical theory of superlattices. Proc. Roy. Soc. London Ser A 150: 552–575. Bibcode:1935RSPSA.150..552B. Zbl 0012.04501. doi:10.1098/rspa.1935.0122.
Baxter, Rodney J. (1982). Exactly solved models in statistical mechanics. Academic Press. ISBN 0-12-083182-1. Zbl 538.60093.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Bethe, H. A. (1935). Statistical theory of superlattices. Proc. Roy. Soc. London Ser A 150: 552–575. Bibcode:1935RSPSA.150..552B. Zbl 0012.04501. doi:10.1098/rspa.1935.0122.

[2] Baxter, Rodney J. (1982). Exactly solved models in statistical mechanics. Academic Press. ISBN 0-12-083182-1. Zbl 538.60093.