Граф Келі

Види графів за їхніми автоморфізмами
відстанево-транзитивний	${\displaystyle \rightarrow }$	відстанево-регулярний	${\displaystyle \leftarrow }$	сильно регулярний
${\displaystyle \downarrow }$
симетричний (дуго-транзитивний)	${\displaystyle \leftarrow }$	t-транзитивний, t ≥ 2
${\displaystyle \downarrow }$(якщо зв'язний)
вершинно- та реберно-транзитивний	${\displaystyle \rightarrow }$	реберно-транзитивний і регулярний	${\displaystyle \rightarrow }$	реберно-транзитивний
${\displaystyle \downarrow }$		${\displaystyle \downarrow }$
вершинно-транзитивний	${\displaystyle \rightarrow }$	регулярний
${\displaystyle \uparrow }$
граф Келі		кососиметричний		асиметричний

Нехай ${\displaystyle G}$ — деяка група і ${\displaystyle S}$ — система її породжуючих (генеруючих) елементів. Визначимо ${\displaystyle T=S\cup S^{-1}.}$

Тоді граф Келі для даної групи Γ = Γ(G, T) будується таким чином:

• Кожному елементу ${\displaystyle g\in G}$ відповідає одна вершина графу.
• Кожному елементу ${\displaystyle t\in T}$ відповідає певний колір c_t
• Для будь-яких ${\displaystyle g\in G}$ та ${\displaystyle t\in T}$ вершини g і gt з'єднуються орієнтованим ребром кольору c_t.

• Графом Келі для нескінченної циклічної групи Z є нескінченний ланцюг.
• Графом Келі для скінченної циклічної групи Z_n є цикл з n вершинами.
• Графом Келі для прямого добутку двох груп є прямий добуток відповідних графів Келі.

• 
  Граф Келі вільної групи з двома твірними a і b
• 
  Граф Келі вільного добутку ${\displaystyle \mathbb {Z} _{2}*\mathbb {Z} _{3}}$
• 
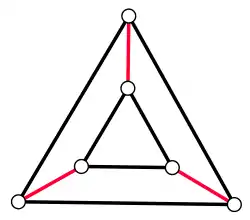  Граф Келі прямого добутку ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{3}}$

• Гіперболічна група
• Ґратка (геометрія)

• Громов М. Л. Гиперболические группы. 2002. — С.160