IEEE P1363
IEEE P1363 — проєкт IEEE зі стандартизації криптосистем з відкритим ключем.
Метою проєкту було поєднання досвіду розробників криптографічних алгоритмів з відкритим ключем і створення єдиної бази їх описів для зручного вибору та застосування.
У підсумку проєкт включає в себе наступні специфікації, розділені за методом шифрування:
- Традиційні криптосистеми з відкритим ключем (IEEE Std 1363—2000 і 1363a-2004)
- Криптосистеми з відкритим ключем на решітках (P1363.1)
- Криптосистеми з відкритим ключем з паролем (P1363.2)
- Особистісне шифрування з відкритим ключем на паруванні (P1363.3)
Описані в стандарті алгоритми також можна умовно розділити за способами застосування:
Через широту охоплення і значної математичної основи стандарт може використовуватися як база для створення національних або галузевих стандартів.
Станом на жовтень 2011 року робочу групу очолює Вільям Уайт з NTRU Cryptosystems, Inc.[1] Він зайняв посаду в серпні 2001. До цього керівниками були Арі Зінгер, також з NTRU (1999—2001), і Барт Каліські з RSA Security (1994—1999).
Історія P1363
Робота над проєктом почалася в 1994 році. До 2001 року робоча група складалася з 31 людини. У 1997 році проєкт був розділений на P1363 і P1363a. У 2000 проєкт був розширений, і вже наприкінці року почалася робота над P1363.1 і P1363.2 [2]. У 2004 році робоча група складалася з 16 чоловік[3].
Традиційні криптосистеми з відкритим ключем (стандарти IEEE 1363—2000 і 1363a-2004)
Дана специфікація включає в себе описи алгоритмів вироблення загального ключа, електронного підпису та безпосередньо шифрування. При цьому використовуються такі математичні методи як факторизація цілих чисел, дискретне логарифмування і дискретне логарифмування в групах точок еліптичних кривих.
Алгоритми вироблення загального ключа
- DL/ECKAS-DH1 і DL/ECKAS-DH2 (англ. Discrete Logarithm/Elliptic Curve Key Agreement Scheme) — алгоритми вироблення загального ключа з використанням дискретного логарифма та еліптичної криптографії у варіанті Діффі — Хеллмана). Включають в себе як стандартний алгоритм Діффі — Хеллмана, побудований на дискретному логарифмировании, так і версію, засновану на еліптичних кривих.
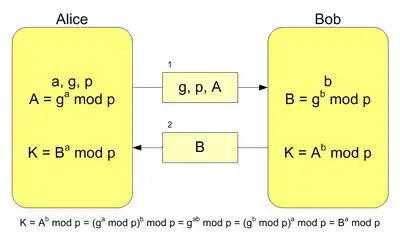Графічне зображення функції, що використовується в алгоритмі Діффі — Хеллмана - DL/ECKAS-MQV — алгоритми вироблення загального ключа з використанням дискретного логарифма та еліптичної криптографії у варіанті MQV. Побудовані на протоколі Діффі-Хеллмана, протоколи MQV вважаються більш захищеним до можливих махінацій з підміною ключів[4].
Алгоритми підпису
- DL/ECSSA (англ. Discrete Logarithm/Elliptic Curve Signature Scheme with Appendix) — алгоритми підпису з використанням дискретного логарифма та еліптичної криптографії з доповненням. Тут чотири основних варіанти: DSA, ECDSA, Nyberg-Rueppel, а також Nyberg-Rueppel на еліптичних кривих.
- IFSSA (англ. Integer Factorization Signature Scheme with Appendix) — алгоритм підпису на цілочисельний факторизації з доповненням, що означає, що функції перевірки справжності треба надати не тільки саму підпис, але також і сам документ. В цей розділ входять дві версії RSA, алгоритм Рабіна (англ. Rabin cryptosystem) і ESIGN, швидкий стандарт, розроблений Nippon Telegraph and Telephone, а також кілька варіантів кодування повідомлення (генерації хеша), званих EMSA. Кілька сполучень мають усталені назви як готові алгоритми. Так, генерація хеша за допомогою EMSA3 з шифруванням RSA1 також має назву PKCS#1 v1.5 RSA signature (за стандартом PKCS, розробленим компанією RSA Security); RSA1 з кодуванням EMSA4 — це RSA-PSS; RSA1 з EMSA2 — алгоритм ANSI X9.31 RSA[5].
- DL/ECSSR (англ. Discrete Logarithm/Elliptic Curve Signature Scheme with Recovery) — алгоритми підпису з використанням дискретного логарифма та еліптичної криптографії з відновленням документа. Це означає, що для належної сторони потрібні тільки відкритий ключ і підпис — саме повідомлення буде відновлено з підпису.
- DL/ECSSR-PV (англ. Discrete Logarithm/Elliptic Curve Signature Scheme with Recovery, Pintsov-Vanstone version) — алгоритми підпису з використанням дискретного логарифма та еліптичної криптографії з відновленням документа, але вже версія Ванстоуна-Пинцова. Цікаво, що Леонід Пінцов — виходець з Росії (закінчував матмех СПБДУ)[6].
- IFSSR (англ. Integer Factorization Signature Scheme with Recovery) — алгоритм з відновленням на цілочисельний факторизації.
Алгоритми шифрування
- IFES (англ. Integer Factorization Encryption Scheme) — один з часто використовуваних алгоритмів, коли дані шифруються RSA, а до цього готуються за допомогою алгоритму OAEP[7].
- DL/ECIES (англ. Discrete Logarithm/Elliptic Curve Integrated Encryption Scheme) — більш стійкий до злому варіант алгоритму Ель-Гамаля (англ. ElGamal encryption), відомий як DHAES[8].
- IFES-EPOC (англ. Integer Factorization Encryption Scheme, EPOC version) — алгоритм EPOC на цілочисельний факторизації.
Криптосистеми з відкритим ключем на решітках (P1363.1)
- Алгоритм шифрування NTRU — алгоритм, що базується на задачі знаходження найкоротшого вектора в решітці. Деякими дослідниками вважається більш швидким[9], а також стійким до злому на квантових комп'ютерах[10], на відміну від стандартних криптосистем з відкритим ключем (наприклад, RSA і алгоритмів еліптичної криптографії).
Криптосистеми з відкритим ключем з паролем (P1363.2)
Сюди входять алгоритми вироблення загального ключа при відомому обом сторонам паролі та алгоритми отримання ключа при відомому пароль.
- BPKAS (англ. Balanced Password-Authenticated Key Agreement Scheme, version PAK) — алгоритм вироблення загального ключа при відомому паролі, коли один і той же пароль використовується як при створенні ключа, так і при його перевірці. У стандарт внесено три версії алгоритму: PAK, PPK і SPEKE
- APKAS-AMP (англ. Augmented Password-Authenticated Key Agreement Scheme, version AMP) — алгоритм вироблення загального ключа при відомому паролі, коли для створення ключа для аутентифікації використовуються різні дані, що побудовані на пароль. 6 версій: AMP, BSPEKE2, PAKZ, WSPEKE, версія SRP (Secure Remote Password) у варіантах 3 і 6, версія SRP у варіанті 5
- PKRS-1 (англ. Password Authenticated Key Retrieval Scheme, version 1) — алгоритм отримання ключа при відомому пароль.
Особистісні криптосистеми з відкритим ключем на паруванні (P1363.3)
В цьому розділі стандарту містяться алгоритми особистісної криптографії, побудовані на різних спарюванні[11]. Цей проєкт був погоджений у вересні 2005, перший повний чернетка[12] з'явився в травні 2008. Станом на жовтень 2011 нових специфікацій не з'являлося.
Аналоги
Іншими проєктами, які займалися каталогізацією криптографічних стандартів є вже згаданий PKCS, створений RSA Security, а також європейський NESSIE і японський CRYPTREC, однак, охоплення IEEE P1363 саме в області криптографії з відкритим ключем значно ширше.
Література
- IEEE Std 1363—2000: IEEE Standard Specifications for Public-Key Cryptography
- IEEE Std 1363a-2004: IEEE Standard Specifications for Public-Key Cryptography — Amendment 1: Additional Techniques
- IEEE P1363.1/D9: Draft Standard for Public-Key Cryptographic Techniques Based on Hard Problems over Lattices (Draft D9, January 2007)
- IEEE P1363.2/D26: Draft Standard for Specifications for Password-based Public Key Cryptographic Techniques (Draft D26, September 2006)
- Jablon D. (01.11.2001). Standard Specifications for Public-Key Cryptography: IEEE P1363 Overview. https://csrc.nist.gov/ (NIST Key Management Workshop). Процитовано 25.11.2017.
Примітки
- IEEE P1363 Contact Information. Архів оригіналу за 4 листопада 2017. Процитовано 25 квітня 2018.
- IEEE P1363 Overview, 2001, с. 5-6, The History.
- The IEEE P1363 Home Page, 2008, Working Group Information.
- INTUIT.ru: Курс: Технологии и продукты ..: Лекция № 13: Проблема аутентификации. Инфраструктура открытых ключей
- RSA Laboratories — 5.3.1 What are ANSI X9 standards?
- Leon A. Pintsov. Архів оригіналу за 23 січня 2011. Процитовано 25 квітня 2018. Текст « Pitney Bowes » проігноровано (довідка)
- RSA, а так ли все просто? / Хабрахабр
- M. Abdalla, M. Bellare, P. Rogaway, «DHAES, An encryption scheme based on the Diffie-Hellman Problem» (Appendix A)
- http://homes.esat.kuleuven.be/~fvercaut/papers/ntru_gpu.pdf
- アーカイブされたコピー. Архів оригіналу за 14 травня 2012. Процитовано 3 лютого 2013.
- Архівована копія. Архів оригіналу за 4 березня 2016. Процитовано 25 квітня 2018.
- Архівована копія. Архів оригіналу за 13 грудня 2016. Процитовано 25 квітня 2018.