Інтеграли Френеля

Нормализовані інтеграли Френеля, S(x) и C(x). На цих кривих аргумент підінтегральних тригонометричних функцій дорівнює ${\displaystyle \pi t^{2}/2}$, а не ${\displaystyle t^{2}}$, як на рисунку вище.

Інтеграли Френеля можуть бути представлені степеневими рядами, що сходяться для всіх x:

${\displaystyle S(x)=\int \limits _{0}^{x}\sin(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+3}}{(4n+3)(2n+1)!}},}$

${\displaystyle C(x)=\int \limits _{0}^{x}\cos(t^{2})\,dt=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+1}}{(4n+1)(2n)!}}.}$

Деякі автори використовують як аргумент тригонометричних підінтегральных функцій ${\displaystyle {\frac {\pi }{2}}t^{2}}$. Отримані функції отримуються із означених вище, шляхом стискання графіка по осі Y у ${\displaystyle {\sqrt {\frac {2}{\pi }}}}$ разів і розтягненням уздовж осі X у стільки ж разів.

Спіраль Корню (x,y)=(C(t), S(t)). Спіраль прямує до центрів отворів за ${\displaystyle t\rightarrow +\infty }$.

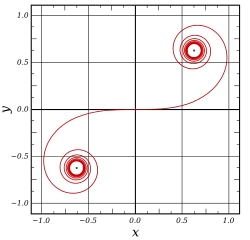
Спіраль Корню, також відома як клотоїда, — це крива, що є параметричним графіком S(t) від C(t). Спіраль Корню була придумана Марі Альфредом Корню для полегшення розрахунку дифракції у прикладних задачах.

Оскільки,

${\displaystyle C\,'(t)^{2}+S\,'(t)^{2}=\sin ^{2}(t^{2})+\cos ^{2}(t^{2})=1,}$

то у такій параметризації дотичний вектор має одиничну довжину, тому t є довгою кривою, що вимірюється від точки (0,0). Звідси, дві гілки спіралі мають нескінченну довжину.

Кривизна цієї кривої у будь-якій точці пропорційна довжині дуги, що розміщується між цією точкою та початком координат. Завдяки цій властивості вона застосовується в будівництві доріг, оскільки кутове прискорення машини, що рухається по цій кривій з постійною швидкістю, буде залишатися сталим.

• C(x) и S(x) — непарні функції x.

• Використовуючи розкладання в ряд, можна побудувати аналітичне продовження інтегралів Френеля на всю комплексну площину. Комплексні інтеграли Френеля виражаються через функцію помилок як

${\displaystyle S(x)={\frac {\sqrt {\pi }}{4}}\left({\sqrt {i}}\,\mathrm {erf} ({\sqrt {i}}\,x)+{\sqrt {-i}}\,\mathrm {erf} ({\sqrt {-i}}\,x)\right)}$

${\displaystyle C(x)={\frac {\sqrt {\pi }}{4}}\left({\sqrt {-i}}\,\mathrm {erf} ({\sqrt {i}}\,x)+{\sqrt {i}}\,\mathrm {erf} ({\sqrt {-i}}\,x)\right)}$.

• Інтегралы Френеля не виражаються через елементарні функції, окрім часткових випадків. Границя цих функцій при ${\displaystyle x\rightarrow \infty }$ дорівнює

${\displaystyle \int \limits _{0}^{\infty }\cos t^{2}\,dt=\int \limits _{0}^{\infty }\sin t^{2}\,dt={\frac {\sqrt {2\pi }}{4}}={\sqrt {\frac {\pi }{8}}}.}$

Обчислення

Контур, що використовується для обчислення граничного значення інтегралів Френеля.

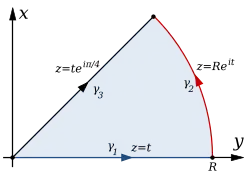
Границі функцій C и S за ${\displaystyle x\rightarrow \infty }$ можуть бути знайдені за допомогою інтегрування по контуру. Для цього обраховується контурний інтеграл функції

${\displaystyle e^{-{\frac {1}{2}}t^{2}}}$

по границі сектору на комплексній площині, що утворений віссю абсцис, променем ${\displaystyle y=x}$, ${\displaystyle x\geqslant 0}$ і колом з радіусом R з центром на початку координат.

При ${\displaystyle R\rightarrow \infty }$ інтеграл по дузі прямує до 0, інтеграл по дійсній осі прямує до значення інтегралу Пуасона

${\displaystyle \int \limits _{0}^{\infty }e^{-{\frac {1}{2}}t^{2}}dt={\sqrt {\frac {\pi }{2}}},}$

і, після деяких перетворень, інтеграл уздовж променя, що залишився, може бути виражений через граничне значення інтегралу Френеля.

• Дифракція Френеля
• Функція Доусона
• Узагальнені інтеграли Френеля

• Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. (См. часть 7) (англ.)

• Weisstein, Eric W. Fresnel Integrals(англ.) на сайті Wolfram MathWorld. (англ.)
• Weisstein, Eric W. Cornu Spiral(англ.) на сайті Wolfram MathWorld. (англ.)
• R. Nave, The Cornu spiral, Hyperphysics (2002) (Використовуює πt²/2 замість t².) (англ.)
• Roller Coaster Loop Shapes. Архів оригіналу за 23 вересня 2008. Процитовано 13 серпня 2008. (англ.)