Алгоритм Воршелла
Алгоритм Воршелла— це ефективний метод побудови транзитивного замкненя на відношенні R. Дія цього алгоритму полягає в перетворенні вхідної матриці MR , яка відображає відношення R, в вихідну транспоновану матрицю MR* на відношенні R*. В свою чергу R* є транзитивним замкненням від відношення R.
Принцип дії алгоритму
Задано відношення R на n-елементарній множині А={a1,a2,a3,…,an}. Алгоритм Воршелла будує послідовність булевих матриць W0,W1, W2, … , Wn, де W0=MR — матриця відношення R. Елементи матриці W(k) позначимо як w(k)ij . Якщо існує шлях із вершини ai до вершини aj такий, що всі його внутрішні вершини містяться в множині {a1,a2,a3,…,an}, утвореній першими k вершинами, то w(k)ij=1, а ні, то w(k)ij =0. Перша й остання вершини такого шляху можуть і не належати множині вершин {a1,a2,a3,…,ak}. Зазначимо, що Wn=MR*. Алгоритм Воршелла ефективно обчислює матрицю W(k) за матрицею W(k-1). Шлях із вершини ai у вершину aj із внутрішніми вершинами в множині {a1,a2,a3,…,ak} існує лише в двох випадках:
1. Якщо існує шлях із вершини ai у вершину aj із внутрішніми вершинами лише в множині {a1,a2,a3,…,ak-1}.

2. Якщо існує шлях із вершини ai у вершину ak та шлях із вершини ak у вершину aj, і кожний із цих шляхів має внутрішні вершини лише в множині {a1,a2,a3,…,ak}
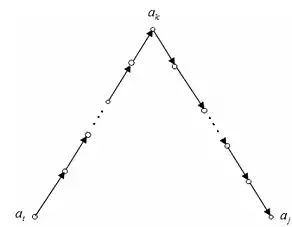
У випадку 1 шлях існує тоді і лише тоді, коли w(k-1)ij=1, у випадку 2 — коли обидва елементи w(k-1)ik та w(k-1)kj дорівнюють 1. Отже, w(k)ij = w(k-1)ij˅(w(k-1)ik ˄w(k-1)kj), k=1,2,…,n.
Формула для практичної реалізації
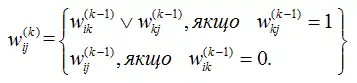
Окрім того очевидно, що в разі i=k дії в першому рядку формули можна не виконувати. Отже,
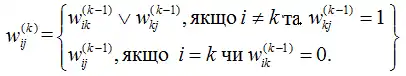
Остання формула дає таке правило переходу від матриці W(k-1) до матриці W(k): для значень i≠k в разі w(k-1)ik=1 замінити i-й рядок матриці W(k-1) на диз'юнкцію i-го й j-го рядків цієї матриці.
Формальний алгоритм Воршелла
(i та j змінюються від 1 до n)
- Виконати W=MR, k=0. Ітерація.
- Виконати k=k+1;
- Для всіх i≠k таких, що wik=1 і для всіх j виконати операцію wij=wij˅wkj. Перевірка закінчення.
- Якщо k=n, то зупинитись. Отримано розв'язок W = MR*. В іншому випадку перейти до кроку 2.
Приклад
Відношення задано матрицею :
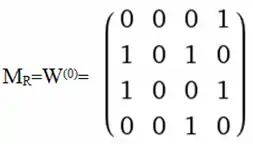
За алгоритмом Уоршалла побудуємо транзитивне замкнення цього відношення. Для k=1 перший рядок залишаємо без змін (i=k), другий і третій рядки замінюємо на диз'юнкцію кожного з них із першим :
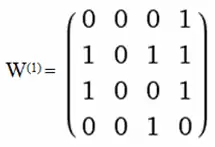
Для k=2 отримаємо, що W(2)=W(1), бо всі елементи другого стовпця матриці W(1) нульові. Далі, для k=3 одержимо :
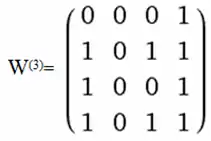
І, нарешті, коли k=4 матимемо остаточний результат — матрицю транзитивного замкнення :
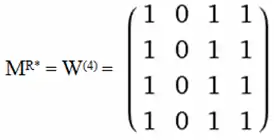
Див. також
Джерела
Rosen, Kenneth H., Discrete Mathematics and its Applications, Third Edition, McGraw-Hill, Inc,1994.