Матриця (математика)

Ма́триця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця), він допускає операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В цій статті вони розглядатися не будуть.

Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтів систем лінійних рівнянь та лінійних перетворень.

Означення та нотація

Матрицею розміру $m\times n$ (m-на-n,або mn-матрицею) називається множина з $mn$ елементів $a_{i,j}$ , розміщених у вигляді прямокутної таблиці з $m$ рядків і $n$ стовпців, а $m$ і $n$ — її розмірністю:

\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}.

де $a_{i,j}$ – елемент матриці; $i$ – номер рядка; $j$ – номер стовпця.

при альтернативному позначенні використовуються великі круглі дужки:

\mathbf {A} =\left({\begin{array}{rrrr}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{array}}\right).

Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпчиками або стовпцями.[1]
Елемент матриці A, що знаходиться на перетині i-го рядка з j-им стовпчиком, називають i,j-им елементом або (i,j)-им елементом A.

Записують це як $a_{i,j}$ чи a[i,j], або, в нотації мови програмування C, A[i][j].

Часто пишуть $\ A:=(a_{i,j})_{n\times m}$ для означення матриці A розмірності n x m, де кожен елемент матриці A[i,j] позначають як a_ij для всіх 1 ≤ i ≤ n та 1 ≤ j ≤ m.

Приклад

Матриця ${\begin{bmatrix}1&2&3\\1&2&7\\4&9&2\\6&2&5\end{bmatrix}}$ є матрицею 4×3. Елемент A[2,3], або $a_{2,3}$ дорівнює 7.

Розмір

Розмір матриці визначає кількість рядків і стовпців, які вона містить. Матрицю із m рядками і n стовпцями називають матрицею m × n або m-на-n матрицею, а самі m і n називають розмірами матриці.

Матриці, які мають лише один рядок називаються векторами-рядками, а ті що мають один стовпець називаються векторами-стовпцями. Матриця з однаковою кількістю рядків і стовпців називається квадратною матрицею. Матриця із нескінченною кількістю рядків або стовпців (або їх обох) називаєтьсяn нескінченною матрицею. У деякому контексті, наприклад, в комп'ютерних програмах, іноді зручно розглядати таку матрицю, що не містить рядків або стовпців, що називається порожньою матрицею.

Назва	Розмір	Приклад	Визначення
Вектор-рядок	1 × n	${\begin{bmatrix}3&7&2\end{bmatrix}}$	Матриця з одним рядком, іноді використовується для представлення вектора
Вектор-стовпець	n × 1	${\begin{bmatrix}4\\1\\8\end{bmatrix}}$	Матриця з одним стовпцем, іноді використовується для представлення вектора
Квадратна матриця	n × n	${\begin{bmatrix}9&13&5\\1&11&7\\2&6&3\end{bmatrix}}$	Матриця з однаковою кількістю рядків і стовпців, іноді використовується для представлення лінійних перетворень у векторному просторі, такі як обертання, відбиття і скіс.

Дії над матрицями

Операція порівняння

Дві матриці $\ A=(a_{i,j})_{m\times n}$ та $\ B=(b_{i,j})_{m\times n}$ називаються рівними $A=B$ , якщо рівні їх відповідні елементи, тобто $a_{i,j}=b_{i,j}$ .

Додавання

Якщо дано дві матриці m-на-n A і B, можемо визначити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, тобто,
(A + B)[i, j] = A[i, j] + B[i, j]. Наприклад,

{\begin{bmatrix}1&3&2\\1&0&0\\1&2&2\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\\2&1&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0&2+5\\1+7&0+5&0+0\\1+2&2+1&2+1\end{bmatrix}}={\begin{bmatrix}1&3&7\\8&5&0\\3&3&3\end{bmatrix}}

Основні властивості операцій додавання матриць:

A + B = B + A (комутативність).
A + (B + C) = (A + B) + C (асоціативність).
A + 0 = A, при будь-якій матриці. Для будь-якої матриці A існує протилежна матриця (-A) , така, що A + (-A) = 0.

Множення на скаляр

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

2{\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\times 1&2\times 8&2\times -3\\2\times 4&2\times -2&2\times 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.

Множення матриць

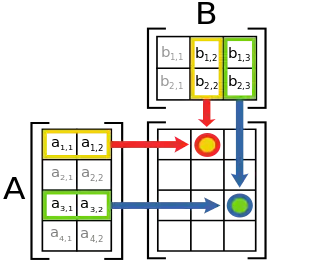
Схематичне зображення добутку AB двох матриць A і B.

Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

Наприклад,

{\begin{bmatrix}1&0&2\\-1&3&1\\\end{bmatrix}}\times {\begin{bmatrix}3&1\\2&1\\1&0\end{bmatrix}}={\begin{bmatrix}(1\times 3+0\times 2+2\times 1)&(1\times 1+0\times 1+2\times 0)\\(-1\times 3+3\times 2+1\times 1)&(-1\times 1+3\times 1+1\times 0)\\\end{bmatrix}}={\begin{bmatrix}5&1\\4&2\\\end{bmatrix}}

Це множення має такі властивості:

(AB)C = A(BC) для всіх матриць A розмірності k-на-m, B розмірності m-на-n і C розмірності n-на-p (асоціативність).
(A + B)C = AC + BC для всіх матриць A і B розмірності m-на-n і матриць C розмірності n-на-k (дистрибутивність).
C(A + B) = CA + CB для всіх матриць A і B розмірності m-на-n і матриць C розмірності k-на-m (дистрибутивність).

Зауваження: комутативність має місце не завжди: для добутку певних матриць A і B може бути AB ≠ BA.

Матриці називають антикомутативними, якщо AB = −BA. Такі матриці є дуже важливими в представленнях алгебр Лі та в представленнях алгебр Кліффорда.

Транспонування

Транспонування матриці A розміром m-на-n утворює матрицю n-на-m A^T (що також позначається як A^tr або ^tA), яка є результатом перевертання рядків у стовпці і навпаки:

(A^T)_i,j = A_j,i.

Приклад: ${\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}$

Розбиття

Матрицю можна розбити на блоки (підматриці) з елементів й присвоїти різним блокам імена. При цьому, коли один блок знаходиться під іншим, то ці блоки повинні мати однакове число стовпців. Коли ж два блоки розташовуються рядом, то вони повинні мати однакове число рядків. Дві блокові матриці, розбиті однаково (тобто відповідні блоки мають однакову розмірність), можна складати поблоково.

Для транспонування блокових матриць необхідно транспонувати кожний блок окремо, а потім транспонувати розташування блоків:

${\begin{pmatrix}M_{1}&...&M_{2}\\...&.&...\\M_{3}&...&M_{4}\end{pmatrix}}^{\mathrm {T} }={\begin{pmatrix}M_{1}^{\mathrm {T} }&...&M_{3}^{\mathrm {T} }\\...&.&...\\M_{2}^{\mathrm {T} }&...&M_{4}^{\mathrm {T} }\end{pmatrix}}$ .

Лінійні перетворення, ранг і транспонування

Матриці можуть представляти лінійні перетворення, оскільки множення матриць відповідає композиції відображень, як це буде показано далі.

Надалі ототожнюватимемо елементи Rⁿ з множиною рядків або матриць n-на-1. Для кожного лінійного відображення f : Rⁿ -> R^m існує єдина матриця A розмірності m-на-n така, що f(x) = Ax для всіх x з Rⁿ. Кажемо, що матриця A «представляє» лінійне відображення f. Тепер, якщо матриця B розмірності k-на-m представляє інше лінійне відображення g : R^m -> R^k, лінійне відображення g o f представлене матрицею BA. Це випливає з зазначеної вище властивості асоціативності множення матриць.

Ранг матриці A — це розмірність образа лінійного відображення, представленого матрицею A. Вона збігається з розмірністю простору, згенерованого рядками матриці A, а також із розміром простору, згенерованого стовпчиками матриці A.

Транспонованою матрицею матриці A розмірності m-на-n є матриця A^tr (також іноді позначають як A^T або ^tA) розмірності n-на-m, яку одержують заміною рядків стовпчиками і навпаки, себто A^tr[i, j] = A[j, i] для всіх індексів i та j. Якщо A описує лінійне відображення відносно двох базисів, матриця A ^tr описує транспозицію лінійного відображення відносно дуальних базисів, див. дуальний простір.

Маємо (A + B)^tr = A^tr + B^tr і (AB)^tr = B^tr * A^tr.

Спеціальні види матриць

У багатьох розділах математики з'являються матриці певної структури. Декілька важливих прикладів:

Квадратна матриця
Одинична матриця
Симетрична матриця — матриця, симетричні елементи яких відносно головної діагоналі (від верхнього лівого до нижнього правого кута) є рівними, себто,

a_i,j = a_j,i.

Нормальна матриця
Ідеальна матриця
Унітарна матриця
Ермітова матриця (або самоспряжена) — матриця, симетричні елементи яких відносно головної діагоналі є комплексно-спряженими один до одного, себто,

a_i,j=a^*_j,i.

Стохастичні матриці — квадратні матриці, стовпчики яких є векторами ймовірності; вони застосовуються для означення Марківських ланцюгів.

Лінійні рівняння

Матриці використовують для компактного представлення систем лінійних рівнянь і роботи з ними. Наприклад, якщо A є матрицею m-на-n, x позначає вектор стовпець (що є матрицею n×1) n змінних x₁, x₂, ..., x_n, і b є вектором-стовпцем m×1, тоді матричне рівняння

\mathbf {Ax} =\mathbf {b}

є еквівалентним наступній системі лінійних рівнянь:

A_{1,1}x_{1}+A_{1,2}x_{2}+\cdots +A_{1,n}x_{n}=b_{1}

\vdots

A_{m,1}x_{1}+A_{m,2}x_{2}+\cdots +A_{m,n}x_{n}=b_{m}

[2]

Із використанням матриць, це можна розв'язати у більш компактній формі ніж виписувати всі ці рівняння окремо. Якщо n = m а рівняння є незалежними, це можливо зробити записавши

\mathbf {x} =\mathbf {A} ^{-1}\mathbf {b}

де A⁻¹ є оберненою матрицею для A. Якщо A не має оберненої матриці, розв'язок, якщо такий існує можна знайти за допомогою [Псевдообернена матриця|псевдооберненої матриці]].

Лінійні перетворення

Вектор заданий 2-на-2 матрицею відповідає сторонам одиничного квадрата, що перетворено на паралелограм.

Матриці і операція множення матриць розкривають свої важливі властивості при застосуванні для лінійних перетворень, що також називають лінійними відображеннями. Дійсна m-на-n матриця A задає лінійне перетворення Rⁿ → R^m і відображає кожен вектор x у Rⁿ у матричний добуток Ax, що в свою чергу є вектором у R^m. Відповідно, кожне лінійне перетворення f: Rⁿ → R^m може здаватися унікальною m-на-n матрицею A: більш детально, (i, j)-входження із A є i^ю координатою f(e_j), де e_j = (0,...,0,1,0,...,0) є одиничним вектором із значенням 1 у j^ій позиції і 0 в інших позиціях. Говорять, що матриця A задає лінійне відображення f, і A називається матрицею перетворення для f.

Наприклад, матрицю 2×2

\mathbf {A} ={\begin{bmatrix}a&c\\b&d\end{bmatrix}}\,

можна розглядати як перетворення одиничного квадрату у паралелограм із вершинами у (0, 0), (a, b), (a + c, b + d), і (c, d). Паралелограм зображений праворуч отримано за допомогою множення A на кожний вектор-стовпець ${\begin{bmatrix}0\\0\end{bmatrix}},{\begin{bmatrix}1\\0\end{bmatrix}},{\begin{bmatrix}1\\1\end{bmatrix}}$ і ${\begin{bmatrix}0\\1\end{bmatrix}}$ по черзі. Ці вектори задають вершини одиничного квадрату.

Наступна таблиця показує декілька 2-на-2 матриць із відповідними лінійними відображеннями у R². Початкова синя фігура відображається у зелену сітку і фігуру. Початок координат (0,0) відмічено чорною точкою.

Горизонтальний скіс при m=1.25.	Відбиття відносно вертикальної осі	Відображення стиснення при r=3/2	Масштабування на коефіцієнт 3/2	Поворот на кут π/6^R = 30°
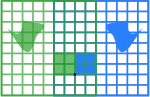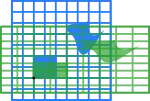${\begin{bmatrix}1&1.25\\0&1\end{bmatrix}}$	${\begin{bmatrix}-1&0\\0&1\end{bmatrix}}$	${\begin{bmatrix}3/2&0\\0&2/3\end{bmatrix}}$	${\begin{bmatrix}3/2&0\\0&3/2\end{bmatrix}}$	${\begin{bmatrix}\cos(\pi /6^{R})&-\sin(\pi /6^{R})\\\sin(\pi /6^{R})&\cos(\pi /6^{R})\end{bmatrix}}$

Квадратна матриця

Квадратна матриця це матриця із однаковою кількістю рядків і стовпців. Матриця n-на-n є квадратною матрицею порядку n. Будь-які дві квадратні матриці однакового порядку можна додавати і множити. Входження a_ii утворюють головну діагональ квадратної матриці. Вони знаходяться на уявній лінії, яка проходить від верхнього лівого кута до нижнього правого кута матриці.

Основні типи

Назва	Приклад для n = 3
Діагональна матриця	${\begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\\\end{bmatrix}}$
Нижньотрикутна матриця	${\begin{bmatrix}a_{11}&0&0\\a_{21}&a_{22}&0\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}$
Верхньотрикутна матриця	${\begin{bmatrix}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{33}\\\end{bmatrix}}$

Діагональна і трикутна матриця

Якщо всі елементи матриці A нижче головної діагоналі дорівнюють нулю, A називають верхньотрикутною матрицею. Аналогічно, якщо всі елементи A вище головної діагоналі дорівнюють нулю, A називають нижньотрикутною матрицею. Якщо всі елементи матриці крім головної діагоналі є нулями , A називають Діагональна матриця.

Одинична матриця

Одинична матриця I_n розміром n є матрицею n-на-n в якій всі елементи головної діагоналі дорівнюють 1 а всі інші елементи дорівнюють 0, наприклад,

I_{1}={\begin{bmatrix}1\end{bmatrix}},\ I_{2}={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\ \cdots ,\ I_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}

Це квадратна матриця порядку n, і також це є особливим випадком діагональної матриці. Вона називається діагональною матрицею, оскільки множення на неї залишає матрицю незмінною:

AI_n = I_mA = A для будь-якої m-на-n матриці A.

Симетричні або кососиметричні матриці

Квадратна матриця A що дорівнює своїй транспонованій матриці, тобто, A = A^T, є симетричною матрицею. Якщо замість того, A дорівнює негативній транспонованій матриці, тобто, A = −A^T, то A є кососиметричною матрицею. У випадку комплексних матриць, поняття симетрії часто заміняється поняттям Ермітової матриці, що задовольняє умові A^∗ = A, де зірочка позначає ермітове-спряження матриці, що є транспонованою комплексною спряженою матриці A.

Відповідно до спектральної теореми, дійсні симетричні матриці і комплексні Ермітові матриці мають власний базис; такий що, кожен вектор можна задати у вигляді лінійної комбінації власних векторів. В обох випадках всі власні значення є дійсними.[3]

Невироджена матриця і її обернена

Квадратна матриця A називається невиродженою або не-сингулярною якщо існує матриця B, така що

AB = BA = I_n ,[4][5]

де I_n n×n є одиничною матрицею із 1-ями на головній діагоналі і 0-ми в інших місцях. Якщо B існує, вона є єдиною і називається оберненою матрицею для A, і позначається як A⁻¹.

Додатноозначена матриця

Додатноозначена матриця	Невизначена матриця
${\begin{bmatrix}1/4&0\\0&1\\\end{bmatrix}}$	${\begin{bmatrix}1/4&0\\0&-1/4\end{bmatrix}}$
Q(x,y) = 1/4 x² + y²	Q(x,y) = 1/4 x² − 1/4 y²
Точки при яких Q(x,y)=1 (Еліпс).	Точки при яких Q(x,y)=1 (Гіпербола).

Симетрична n×n-матриця A називається додатноозначеною якщо для всіх не нульових векторів x ∈ Rⁿ відповідна квадратична форма, що задається як

f(x) = x^TA x

утворює в результаті лише додатні значення для будь-якого вхідного вектору x. Якщо f(x) приводить до утворення лише від'ємних значень тоді A є від'є́мно ви́значеною; якщо f утворює як додатні так і від'ємні значення тоді A є невизначеною.[6] Якщо квадратична форма f породжує лише не-від'ємні значення (додатні або нуль), симетрична матриця називається додатно напіввизначеною. Таблиця праворуч показує два варіанти для матриць 2-на-2.

Якщо в якості входів задати два різні вектори буде отримана білінійна форма, що пов'язана із A:

B_A (x, y) = x^TAy.[7]

Ортогональна матриця

Ортогональна матриця це квадратна матриця із дійсними елементами, чиї стовпці і рядки є ортогональними одиничними векторами (тобто, ортонормованими векторами). Це рівносильно тому, що матриця A є ортогональною якщо її транспонована матриця дорівнює її оберненій матриці:

A^{\mathrm {T} }=A^{-1},\,

що тягне за собою

A^{\mathrm {T} }A=AA^{\mathrm {T} }=I_{n},\,

де I є одиничною матрицею розміром n.

Слід матриці

Слід, tr(A) квадратної матриці A є сумою елементів її діагоналі. Хоча операція множення не є комутативною, слід добутку двох матриць не залежить від порядку операцій:

tr(AB) = tr(BA).

Це випливає прямо із визначення операції множення матриць:

\operatorname {tr} ({\mathsf {AB}})=\sum _{i=1}^{m}\sum _{j=1}^{n}A_{ij}B_{ji}=\operatorname {tr} ({\mathsf {BA}}).

Також, слід матриці буде дорівнювати сліду її транспонованої матриці, тобто,

tr(A) = tr(A^T).

Визначник

Лінійне перетворення R² задане наведеною матрицею. Визначник матриці дорівнює −1, площа зеленого паралелограма праворуч дорівнює 1, але відображення має обернену орієнтацію.

Визначник (визначник) det(A) або |A| квадратної матриці A, що визначає деякі властивості матриці. Матриця є невиродженою, тоді й лише тоді коли її детермінант не нульовий. Його абсолютне значення дорівнює площі (у R²) або об'єму (у R³) відображення одиничного квадрата (або куба), а його знак відповідає орієнтації відповідного лінійного відображення: визначник є додатнім тоді і лише тоді, коли орієнтація зберігається.

Визначник матриці 2-на-2 дорівнює

\det {\begin{bmatrix}a&b\\c&d\end{bmatrix}}=ad-bc.

Детермінант матриці 3-на-3 матиме 6 термів (Правило Саррюса). Більш складна Формула Лейбніца узагальнює ці дві формули до всіх вимірів.[8]

Визначник добутку квадратних матриць дорівнює добутку їх визначників:

det(AB) = det(A) · det(B).[9]

Додавання до рядка іншого рядка помноженого на деяке значення, або додавання стовпця до іншого стовпця, не змінює детермінанта матриці. Заміна місцями двох рядків або стовпців приводить до зміни знаку визначника, тобто множення його на −1.[10] Використовуючи ці операції, можна звести будь-яку матрицю до нижньої (або верхньої) трикутної матриці, а для таких матриць визначник буде дорівнювати добутку елементів головної діагоналі; що є методом розрахунку визначника будь-якої матриці. З рештою, розклад Лапласа дозволяє виразити визначник через мінори, тобто, детермінанти менших матриць.[11] Це розкладання можна використовувати для рекурсивного визначення визначника, що можна розглядати як рівнозначний до формули Лейбніца. Визначник використовується для розв'язання систем лінійних рівнянь за допомогою метода Крамера.[12]

Матриці в абстрактній алгебрі

Якщо взяти кільце R, можемо розглядати множину M(m,n, R) усіх матриць m на n з елементами з R. Додавання та множення цих матриць може бути означене, як у випадку дійсних чи комплексних матриць. Множина M(n, R) усіх квадратних матриць n на n над кільцем R сама є кільцем, ізоморфним до кільця ендоморфізмів правого R-модуля Rⁿ.

Також, якщо елементи беруться з напівкільця S, додавання та множення матриць можна означити звичайним чином. Множина всіх квадратних матриць n×n над S сама є напівкільцем. Зважте на те, що алгоритми множення матриць, такі як алгоритм Штрассена, взагалі застосовні лише до матриць над кільцями і не працюють для матриць над напівкільцями, що не є кільцями.

Якщо R є комутативним кільцем, тоді M(n, R) є унітарною асоціативною алгеброю над R. Також має сенс означити детермінант квадратних матриць, застосовуючи формулу Лейбніца. Матриця має обернену тоді й лише тоді, коли її визначник як елемент R має обернений елемент в R.

Усі твердження цієї статті для дійсних та комплексних матриць справджуються і для матриць над довільним полем.

Матриці над кільцем поліномів є важливими у вивченні теорії керування.

Історія

Вивчати матриці почали досить давно. Латинські квадрати та магічні квадрати були відомі ще в доісторичні часи.

Китайський текст «Математика в дев'яти книгах» (написаний ще до нашої ери) містить приклади використання матриць для розв'язання системи рівнянь, включаючи поняття визначника, ще задовго до введення визначників японським математиком Такакадзу Секі (1683) та німецьким математиком Лейбніцем (1693). Крамер розвинув цю теорію, ввівши правило Крамера 1750 р. Карл Фрідріх Ґаус та Вільгельм Йордан розробили метод Ґауса — Йордана знаходження оберненої матриці 1800 р.

Термін «матриця» уперше було запроваджено 1848 р. Дж. Дж. Сильвестром. Кейлі, Гамільтон, Ґрассман, Фробеніус, фон Нойман та інші видатні математики зробили свій внесок у теорію матриць.

Див. також

Навчальні матеріали

(укр.) Вступ до лінійної алгебри: матриці та дії з ними. Лекція 1 на YouTube, М. Іоргов (Інститут теоретичної фізики НАН України)
(укр.) Вступ до лінійної алгебри: матриці та дії з ними. Лекція 2 на YouTube, М. Іоргов (Інститут теоретичної фізики НАН України)

Примітки

Рицар, Богдан; Сніцарук, Леонід; Мисак, Роман (2015 – 2018). Українсько-англійський словник з радіоелектроніки. e2u.org.ua.
Brown 1991, I.2.21 and 22
Horn & Johnson 1985, Theorem 2.5.6
Brown 1991, Definition I.2.28
Brown 1991, Definition I.5.13
Horn & Johnson 1985, Chapter 7
Horn & Johnson 1985, Example 4.0.6, p. 169
Brown 1991, Definition III.2.1
Brown 1991, Theorem III.2.12
Brown 1991, Corollary III.2.16
Mirsky 1990, Theorem 1.4.1
Brown 1991, Theorem III.3.18

Література

Узагальнена еквівалентність матриць і їх наборів та факторизація матриць над кільцями : монографія / В. М. Петричкович ; НАН України, Ін-т приклад. проблем механіки і математики ім. Я. С. Підстригача. – Львів : ІППММ, 2015. – 312 с. – Бібліогр.: с. 285-311 (245 назв). – ISBN 978-96-02-7619-2
Гантмахер Ф. Р. Теория матриц. — М. : Физматлит, 2010. — 560 с.
Голуб Дж., ван Лоун Ч. Матричные вычисления. — М. : Мир, 1999. — 548 с.
Ланкастер П. Теория матриц. — М. : Наука, 1982. — 272 с.

Посилання

Матриці, дії над матрицями // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 5-7. — 594 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Рицар, Богдан; Сніцарук, Леонід; Мисак, Роман (2015 – 2018). Українсько-англійський словник з радіоелектроніки. e2u.org.ua.

[2] Brown 1991, I.2.21 and 22

[3] Horn & Johnson 1985, Theorem 2.5.6

[4] Brown 1991, Definition I.2.28

[5] Brown 1991, Definition I.5.13

[6] Horn & Johnson 1985, Chapter 7

[7] Horn & Johnson 1985, Example 4.0.6, p. 169

[8] Brown 1991, Definition III.2.1

[9] Brown 1991, Theorem III.2.12

[10] Brown 1991, Corollary III.2.16

[11] Mirsky 1990, Theorem 1.4.1

[12] Brown 1991, Theorem III.3.18