Транспонована матриця

Транспонована матриця — матриця ${\displaystyle A^{T}}$, що виникає з матриці ${\displaystyle A}$ в результаті унарної операції транспонування: заміни її рядків на стовпчики.

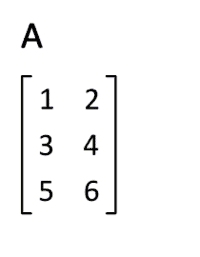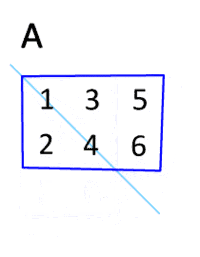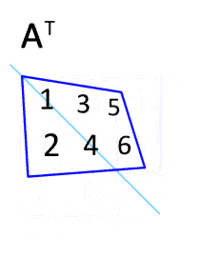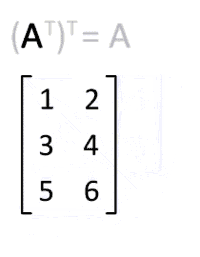
Формально, транспонована матриця ${\displaystyle \ A^{T}=(b_{ij})}$ для матриці ${\displaystyle \ A=(a_{ij})}$ визначається як

${\displaystyle \ b_{ij}=a_{ji},\quad i={\overline {1,n}},\quad j={\overline {1,m}}.}$

Наприклад:

${\displaystyle {\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3\\2&4\end{bmatrix}}}$      та      ${\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}}$