Алгоритм швидкої оболонки

Алгоритм швидкої оболонки — метод обчислення опуклої оболонки скінченної множини точок на площині. Використовує підхід «розділяй та володарюй», який полягає в тому, що задача розбивається на підзадачі приблизно однакового розміру. Аналогічний метод, використовується в алгоритмі швидкого сортування, звідси така назва.

Анімація побудови опуклої оболонки

Складність алгоритму буде $O(n*\log(n))$ , якщо кількість елементів підзадач буде лінійно зменшуватись зі сталим коефіцієнтом k<1. В найгіршому випадку швидкість буде O(n²) (квадратична).

Алгоритм

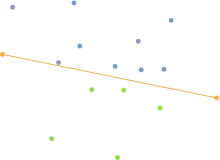
Кроки 1-2: Через крайні ліву та праві точки проводимо лінію, яка поділить точки на дві множини

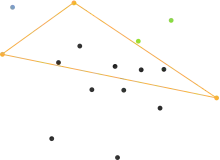
Кроки 3-5: Знаходження максимальної відстані до точки, яка знаходиться не всередині трикутника та не на його межі

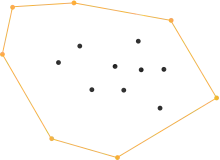
Кроки 6: Рекурсія, поки жодної точки, що задовольняє умовам, не залишиться

Алгоритм можна розбити на наступні етапи:

Знайти точки з мінімальною і максимальною $x$ координатою, вони зобов'язані бути частиною опуклої оболонки.
Використовуючи лінію, утворену двома точками розділити всю множину точок на дві підмножини, які будуть оброблятися рекурсивно.
Визначити точку, на одній стороні лінії, з максимальною відстанню від лінії. Знайдені до цього дві точки утворюють з цією точкою трикутник з найбільшою площею.
Точки, що лежать всередині цього трикутника не може бути частиною опуклої оболонки і, отже, можуть бути проігноровані в наступних кроках.
Повторіть попередні два кроки для двох ліній, утвореного трикутника (окрім початкової лінії).
Продовжуйте робити так доти, поки більше точок не залишиться, у кінці рекурсії, вибрані точки, складуть опуклу оболонку.

Переваги

Алгоритм легко розпаралелити.
Алгоритм узагальнюється на довільну розмірність.

Недоліки

Висока квадратична трудомісткість в найгіршому випадку.

Псевдокод

procedure otochka(tochky)
	begin
		A := крайня ліва точка
		B := крайня права точка
		s1 := множина точок з правої сторони AB
		s2 := множина точок з лівої сторони AB

		return [A] + QuickHull(A, B, s1) + [B] + QuickHull(B, A, s2);
	end;

procedure QuickHull(A, B, tochky)
	begin
		C := найбільш віддалена точка від прямої AB
		s1 := множина точок, яка знаходиться на праворуч від відрізка AC
		s2 := множина точок, яка знаходиться на праворуч від відрізка CB

		return QuickHull(A, C, s1) + [C] + QuickHull(C, B, s2);
	end;

Див. також

Алгоритми обчислення опуклої оболонки

Посилання

Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 грудня 1996). The quickhull algorithm for convex hulls. ACM Transactions on Mathematical Software 22 (4): 469–483. doi:10.1145/235815.235821.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.