Опукла оболонка
Опукла оболонка (англ. Convex hull) множини точок X на евклідовій площині або у просторі — це мінімальна опукла множина, що містить X.
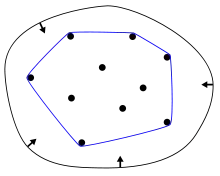
В обчислювальній геометрії, прийнято використовувати термін «опукла оболонка» для межі мінімальної опуклої множини, що містить дану не порожню скінченну множину точок на площині. Для скінченної множини точок, опукла оболонка являє собою ламану лінію.
Властивості
- — опукла множина тоді і тільки тоді, коли .
- Для довільної підмножини лінійного простору існує єдина опукла оболонка — перетин усіх опуклих множин, що містять .
- При цьому
- Більш того, якщо вимірність простору дорівнює тоді вірна наступна теорема Каратеодорі про опуклу оболонку:
- При цьому
- Опуклою оболонкою скінченного набору точок на площині є опуклий плоский багатокутник (у вироджених випадках — відрізок або точка), причому його вершини є підмножиною похідного набору точок. Аналогічний факт вірний і для скінченного набору точок в багатовимірному просторі.
- Опукла оболонка дорівнює перетину всіх півпросторів, що містять .
- Для двох опуклих множин, які не перетинаються, завжди існує гіперплощина, що їх розділяє.
Варіації і узагальнення
Опуклою оболонкою функції f називають таку функцію , що
- ,
де epi f — надграфік функції f.
Варто зауважити зв'язок поняття опуклої оболонки функції з перетворенням Лежандра неопуклих функцій. Нехай f * — перетворення Лежандра функції f. Тоді якщо — власна функція (приймає скінченні значення на непорожньой множині), тоді
— опукле замкнення f, тобто існує функція, надграфік якої є замкненням надграфіка f.
Посилання
- Weisstein, Eric W. Convex Hull(англ.) на сайті Wolfram MathWorld.
- «Convex Hull» by Eric W. Weisstein, Wolfram Demonstrations Project, 2007.
