Алгоритми обчислення опуклої оболонки

Кожному числу ${\displaystyle x_{i}}$ відповідає точка на параболі з координатами ${\displaystyle (x_{i},x_{i}^{2})}$. Таким чином задача побудови ОО еквівалентна задачі впорядкування точок.

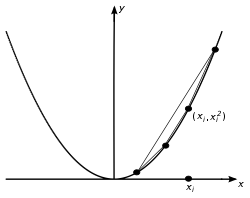
Для скінченої множини точок на площині нижня межа обчислювальної складності находження опуклої оболонки у вигляді опуклого многокутника є тією ж, що й в задачі сортування з подальшим зведенням. Це унаочнює такий приклад.

Для множини ${\displaystyle x_{1},\dots ,x_{n}}$ чисел, які треба відсортувати, розглянемо множину ${\displaystyle (x_{1},x_{1}^{2}),\dots ,(x_{n},x_{n}^{2})}$ точок площини. Так як, вони лежать на параболі, яка є опуклою кривою, легко бачити, що вершини опуклої оболонки, що проходяться вздовж межі, створюють відсортовану множину чисел ${\displaystyle x_{1},\dots ,x_{n}}$. Очевидно, для описаного перетворення чисел на точки і отримання їх відсортованого порядку потребується лінійний час. З цієї причини в загальному випадку опукла оболонка n точок не може бути обчислена швидше, ніж проведено їх сортування.

Стандартна Ω(n log n) нижня межа сортування доведена в обчислювальній моделі дерева прийняття рішень, в якому виконуються тільки порівняння, але не арифметичні дії; однак в цій моделі опуклі оболонки не можуть бути обчислені взагалі. Сортування також потребує час Ω(n log n) в обчислювальній моделі алгебраїчного дерева прийняття рішень, моделі, що більш підходить для опуклих оболонок, і в цих моделях опуклі оболонки також потребують час Ω(n log n).[1] Однак в моделях комп'ютерної арифметики дозволяється сортувати числа швидше, ніж за час O(n log n), наприклад, при використанні алгоритмів цілочисельного сортування, пласкі опуклі оболонки також можуть бути обчислені швидше: Алгоритм Грехема для опуклих оболонок містить один крок сортування після якого йде лінійний об'єм додаткової роботи.

Відомі алгоритми обчислення опуклої оболонки, наведені нижче, відсортовано за датою їх першої публікації. Обчислювальна складність кожного алгоритму наведена в термінах числа вхідних точок n і числа точок оболонки h. В найгіршому випадку h дорівнюватиме n.

• Алгоритм Джарвіса — O(nh)
  Один з найпростіших (також з найефективнішим використанням часу в найгіршому випадку) плоских алгоритмів. Винайдений Чандом і Капуром в 1970 і Р. А. Джарвісом в 1973 роках. Він має обчислювальну складність O(nh). В найгіршому випадку обчислювальна складність складає O(n²).

• Алгоритм Грехема — O(n log n)
  Дещо більш складний, але значно більш ефективний алгоритм, опублікований Рональдом Гремом в 1972 році. Якщо точки вже відсортовані за однією з координат о за кутом до фіксованого вектора, алгоритм потребує час O(n).

• Алгоритм швидкої оболонки
  Винайдений незалежно в 1977 У. Едді та в 1978 А. Бікатом. Як алгоритм швидкого сортування має очікувану складність обчислень O(n log n), але може погіршуватися до Θ(nh) = O(n²) в найгіршому випадку.

• Розділяй і володарюй — O(n log n)
  Інший O(n log n) алгоритм, опублікований в 1977 році Франко Препарата і Хонгом. Цей алгоритм є також придатним для тривимірного випадку.

• Монотонний ланцюг або Алгоритм Ендрю — O(n log n)
  Опубліковано в 1979 А. М. Ендрю. Алгоритм можна розглядати як варіант алгоритму Грехема який сортує точки в лексикографічному порядку за їх координатами. В разі, якщо вхідні точки вже відсортовані, алгоритм потребує час O(n).

• Інкрементальний алгоритм обчислення опуклої оболонки — O(n log n)
  Опубліковано в 1984 році М. Келей.

• Алгоритм Кіркпатрика — Зейделя — O(n log h)
  Перший оптимальний чутливий до вихідних даних алгоритм, він використовує техніку «шлюб перед завоюванням». Опубліковано Девідом Кіркпатріком і Реймундом Зейделем в 1986.

• Алгоритм Чена — O(n log h)
  Простіший оптимальний чутливий до вихідних даних алгоритм винайдений Тімоті Ченом в 1996 році.