Базис (математика)
Ба́зисом (дав.-гр. βασις, основа) векторного простору називається впорядкований набір векторів , якщо кожний вектор із можна однозначно представити у вигляді лінійної комбінації:
.svg.png.webp)
Коефіцієнти кільця називаються координатами вектора відносно базису [1]. Ця рівність зазвичай записується скорочено:
. Тобто так само, як і для запису матриць.
Якщо та - деяке дійсне число, то
Таким чином, кожний вектор простору повністю визначається своїми координатами, тобто впорядкованою трійкою дійсних чисел,а операції над векторами простору зводяться до операцій над впорядкованими трійками дійсних чисел. Таким чином, з алгебричної точки зору вектори простору можна вважати впорядкованими трійками чисел[2].
Представлення вектора у вигляді лінійної комбінації базисних векторів називається розкладанням вектора по даному базису.
Кількість векторів базису не залежить від вибору базисних векторів і дорівнює розмірності простору і позначається Існують простори як із скінченним, так й нескінченним базисом. Наприклад, n-вимірний еквлідовий простір.
Вектори базису є лінійно незалежними.
Обертання

Набір лінійно незалежних векторів можна неперервно перетворювати, тому ні у якій проміжній конфігурації об'єм не перетвориться на нуль, або до набору (правий базис), або до набору (лівий базис). Зокрема, перетворення здійснюється як поворот у площині, натягнутій на вектори на кут
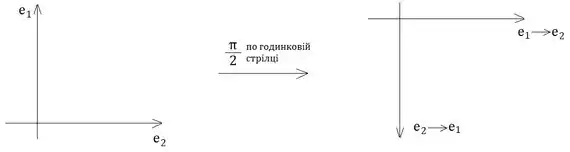
Знак у формулі, наведеній під малюнком, визначається парністю перестановки[3].
Існує застереження щодо складання обертань: трьохвимірні обертання не комутують[4].
Приклад
Вектори ei = (0, …, 1, …, 0), 1 ≤ i ≤ n утворюють базис в .
Примітки
- А. И. Кострикин, Ю. И. Манин. Линейная алгебра и геометрия.
- С.Т.Завало, В.Н.Костарчук, Б.И.Хацет - Алгебра и теория чисел.
- М.Г.Иванов - Механика и теория поля.
- Moti Ben-Ari - A Tutorial on Euler Angles and Quaternions.
Джерела
- Гельфанд И. М. Лекции по линейной алгебре. — 5-е. — Москва : Наука, 1998. — 320 с. — ISBN 5791300158.(рос.)
- Мальцев А. И. Основы линейной алгебры. — 3-е изд. — Новосибирск : Наука, 1970. — 400 с.(рос.)