Безлад (перестановка)

В комбінаториці безладом називається перестановка без нерухомих точок, тобто жодний елемент не залишається на початковому місці.

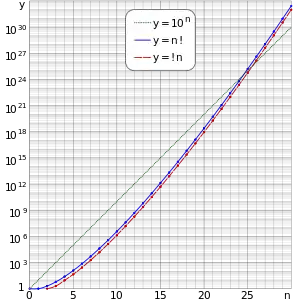
Число можливих перестановок та безладів для n елементів. n! (n факторіал) — це число n-перестановок; !n (n субфакторіал) — це число безладів — n-перестановок, в яких усі n елементів змінюють свої початкові місця.

Таблиця значень
$n$	Перестановка, $n!$	Безлад, $!n$	${\frac {!n}{n!}}$
0	1 =1×10⁰	1 =1×10⁰	= 1
1	1 =1×10⁰	0	= 0
2	2 =2×10⁰	1 =1×10⁰	= 0.5
3	6 =6×10⁰	2 =2×10⁰	≈0.33333 33333
4	24 =2.4×10¹	9 =9×10⁰	= 0.375
5	120 =1.20×10²	44 =4.4×10¹	≈0.36666 66667
6	720 =7.20×10²	265 =2.65×10²	≈0.36805 55556
7	5 040 ≈5.04×10³	1 854 ≈1.85×10³	≈0.36785 71429
8	40 320 ≈4.03×10⁴	14 833 ≈1.48×10⁴	≈0.36788 19444
9	362 880 ≈3.63×10⁵	133 496 ≈1.33×10⁵	≈0.36787 91887
10	3 628 800 ≈3.63×10⁶	1 334 961 ≈1.33×10⁶	≈0.36787 94643
11	39 916 800 ≈3.99×10⁷	14 684 570 ≈1.47×10⁷	≈0.36787 94392
12	479 001 600 ≈4.79×10⁸	176 214 841 ≈1.76×10⁸	≈0.36787 94413
13	6 227 020 800 ≈6.23×10⁹	2 290 792 932 ≈2.29×10⁹	≈0.36787 94412
14	87 178 291 200 ≈8.72×10¹⁰	32 071 101 049 ≈3.21×10¹⁰	≈0.36787 94412
15	1 307 674 368 000 ≈1.31×10¹²	481 066 515 734 ≈4.81×10¹¹	≈0.36787 94412
16	20 922 789 888 000 ≈2.09×10¹³	7 697 064 251 745 ≈7.70×10¹²	≈0.36787 94412
17	355 687 428 096 000 ≈3.56×10¹⁴	130 850 092 279 664 ≈1.31×10¹⁴	≈0.36787 94412
18	6 402 373 705 728 000 ≈6.40×10¹⁵	2 355 301 661 033 953 ≈2.36×10¹⁵	≈0.36787 94412
19	121 645 100 408 832 000 ≈1.22×10¹⁷	44 750 731 559 645 106 ≈4.48×10¹⁶	≈0.36787 94412
20	2 432 902 008 176 640 000 ≈2.43×10¹⁸	895 014 631 192 902 121 ≈8.95×10¹⁷	≈0.36787 94412
21	51 090 942 171 709 440 000 ≈5.11×10¹⁹	18 795 307 255 050 944 540 ≈1.88×10¹⁹	≈0.36787 94412
22	1 124 000 727 777 607 680 000 ≈1.12×10²¹	413 496 759 611 120 779 881 ≈4.13×10²⁰	≈0.36787 94412
23	25 852 016 738 884 976 640 000 ≈2.59×10²²	9 510 425 471 055 777 937 262 ≈9.51×10²¹	≈0.36787 94412
24	620 448 401 733 239 439 360 000 ≈6.20×10²³	228 250 211 305 338 670 494 289 ≈2.28×10²³	≈0.36787 94412
25	15 511 210 043 330 985 984 000 000 ≈1.55×10²⁵	5 706 255 282 633 466 762 357 224 ≈5.71×10²⁴	≈0.36787 94412
26	403 291 461 126 605 635 584 000 000 ≈4.03×10²⁶	148 362 637 348 470 135 821 287 825 ≈1.48×10²⁶	≈0.36787 94412
27	10 888 869 450 418 352 160 768 000 000 ≈1.09×10²⁸	4 005 791 208 408 693 667 174 771 274 ≈4.01×10²⁷	≈0.36787 94412
28	304 888 344 611 713 860 501 504 000 000 ≈3.05×10²⁹	112 162 153 835 443 422 680 893 595 673 ≈1.12×10²⁹	≈0.36787 94412
29	8 841 761 993 739 701 954 543 616 000 000 ≈8.84×10³⁰	3 252 702 461 227 859 257 745 914 274 516 ≈3.25×10³⁰	≈0.36787 94412
30	265 252 859 812 191 058 636 308 480 000 000 ≈2.65×10³²	97 581 073 836 835 777 732 377 428 235 481 ≈9.76×10³¹	≈0.36787 94412

Число безладів множини з n елементів, зазвичай позначається D_n, d_n, або !n, і називається «числом безладів» або «числом Монмора». (Ці числа узагальнюються числами, що відповідають числу зустрічей.) Функція субфакторіал (не плутайте з факторіалом n!) ставить у відповідність числу n число !n.[1] Не існує стандартного позначення для субфакторіалу. Інколи позначають n¡ замість !n.[2]

Задача підрахунку числа безладів була уперше розглянута П'єром де Монмором[3] у 1708; він розв'язав її у 1713, як це зробив Микола I Бернуллі приблизно в той же час.

Приклади

Перевірка робіт

Припустимо, що професор дав чотирьом студентам (назвемо їх A, B, C і D) контрольну, а потім запропонував їм перевірити її один у одного. Звісно, жоден студент не повинен перевіряти свою контрольну. Скільки у професора варіантів розподілу контрольних, в яких жодному студенту не дістанеться своя робота? З усіх 24-х перестановок (4!) для повернення робіт, нам підходять тільки 9 безладів:

BADC, BCDA, BDAC,

CADB, CDAB, CDBA,

DABC, DCAB, DCBA.

У будь-який інший перестановці цих 4-х елементів, принаймні один студент отримує свою контрольну на перевірку.

Задача про листи

Обчислення кількості безладів є популярною задачею в олімпіадній математиці, яка зустрічається в різних формулюваннях таких як завдання про безлад, завдання про листи, завдання про зустрічі і т. д.

Якщо

n

листів випадковим чином покласти в

n

різних конвертів, то яка ймовірність, що якийсь лист потрапить в свій конверт?

Відповідь дається виразом

1-{\frac {!n}{n!}}\approx 1-{\frac {1}{e}}

Таким чином, відповідь слабо залежить від кількості листів і конвертів і приблизно дорівнює константі $1-{\frac {1}{e}}\approx 0,63212$ .

Кількість безладів

Кількість всіх безладів порядку n може бути обчислено за допомогою принципу включення-виключення і дається виразом:

!n=n!-{\frac {n!}{1!}}+{\frac {n!}{2!}}-{\frac {n!}{3!}}+\dots +(-1)^{n}{\frac {n!}{n!}}=\sum _{k=0}^{n}(-1)^{k}{\frac {n!}{k!}}

яке називається субфакторіалом числа n.

Кількість безладів $!n=d(n)$ задовольняє рекурсивним співвідношенням

$d(n)=(n-1)[d(n-1)+d(n-2)]$

і

$d(n)=nd(n-1)+(-1)^{n}$

де $d(1)=0$ і $d(2)=1$

З огляду на те, що $\sum _{k=0}^{\infty }(-1)^{k}{\frac {1}{k!}}={\frac {1}{e}}$ , значення $!n$ зі збільшенням $n$ веде себе як ${\frac {n!}{e}}$ . Більше того, при $n>0$ його можна представити як результат округлення числа ${\frac {n!}{e}}$ .

Див. також

Парадокс днів народження

Примітки

Назва «субфакторіал» походить від William Allen Whitworth; див. Cajori, Florian (2011). A History of Mathematical Notations: Two Volumes in One. Cosimo, Inc.,. с. 77. ISBN 9781616405717..
Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics (1994), Addison-Wesley, Reading MA. ISBN 0-201-55802-5
de Montmort, P. R. (1708). Essay d'analyse sur les jeux de hazard. Paris: Jacque Quillau. Seconde Edition, Revue & augmentée de plusieurs Lettres. Paris: Jacque Quillau. 1713.

Посилання

Виведення формули кількості безладів трьома способами (англ.)
Р. Стенлі. Перелічувальна комбінаторика. — М. : Мир, 1990. — С. 107-108.
Baez, John (2003). Let's get deranged!.
Bogart, Kenneth P. and Doyle, Peter G. (1985). Non-sexist solution of the ménage problem.
Dickau, Robert M. Derangement diagrams. Figures Using Mathematica.
Hassani, Mehdi. Derangements and Applications. Journal of Integer Sequences (JIS), Volume 6, Issue 1, Article 03.1.2, 2003.
Weisstein, Eric W. Derangement. MathWorld–A Wolfram Web Resource.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Назва «субфакторіал» походить від William Allen Whitworth; див. Cajori, Florian (2011). A History of Mathematical Notations: Two Volumes in One. Cosimo, Inc.,. с. 77. ISBN 9781616405717..

[2] Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics (1994), Addison-Wesley, Reading MA. ISBN 0-201-55802-5

[3] Montmort, P. R. (1708). Essay d'analyse sur les jeux de hazard. Paris: Jacque Quillau. Seconde Edition, Revue & augmentée de plusieurs Lettres. Paris: Jacque Quillau. 1713.