Вейвлет

Вейвлет-перетворення (wavelet, вейвлет, хвильки, хвилькові перетворення). Усі вейвлет-перетворення розглядають функцію (взяту як функцією від часу) у термінах коливань, локалізованих за часом (простором) і частотою. Локальність у просторі означає, що енергія хвильок (вейвлетів) сконцентрована на скінченному інтервалі, так звана функція на компактному носії. Частотна локалізація означає, що перетворення Фур'є хвильки локалізоване. Частотна локалізація функції зводиться до понять гладкості та кількості зникаючих моментів. Вейвлет-перетворення звичайно поділяють на дискретне вейвлет-перетворення (DWT) та неперервне вейвлет-перетворення (CWT).

Застосування вейвлет-перетворень

Дискретне вейвлет-перетворення (DWT) звичайно використовується для кодування сигналів, у той час як CWT для аналізу сигналів. Саме тому, DWT широко застосовується в інженерній справі і комп'ютерних науках, а CWT у наукових дослідженнях фізичних процесів. Вейвлет-перетворення в наш час^[коли?] взяті на озброєння для величезної кількості різнопланових застосувань, нерідко заміняючи звичайне перетворення Фур'є у багатьох прикладних задачах. Ця зміна парадигми спостерігається в багатьох галузях фізики, включаючи молекулярну динаміку, астрофізику, квантовій механіці, геофізиці, оптиці, механіці рідини та у багатьох інших областях, включаючи обробку зображень, аналізу кров'яного тиску, пульсу та ЕКГ, аналіз ДНК, дослідження білків, вивчення клімату, загальну обробку сигналів, розпізнавання мови, комп'ютерну графіку і мультифрактальний аналіз. Таке широке використання вейвлет-перетворень забезпечується можливістю побудувати на їх основі методи, що потребуватимуть O(N) операцій, на противагу методів Фур'є-перетворень, де кількість операцій не менша за O(NlogN).

Історія

До розроблення вейвлетів призвели декілька незалежних шляхів міркувань, що почалися з робіт Хаара, який на початку двадцятого століття поставив запитання: «Чи існує інша ортонормальна система $h_{0}(x),h_{1}(x),...,h_{n}(x),...$ функцій, визначених на проміжку [0, 1], таких, що довільну функцію $f(x)\in C[0,1]$ можна розвинути у суму вигляду $<f,h_{0}>h_{0}(x)+...+<f,h_{n}>h_{n}(x)+...$ , і що вона буде збіжною до $f(x)$ єдиним чином на [0, 1]?» Як виявилося таких систем можна побудувати нескінченну кількість. У 1909 році Хаар запропонував найпростіший розв'язок і тим самим відкрив шлях, що веде до вейвлет (wavelet). Ортонормальна система Хаара будується починаючи з базисної функції $h(x)=1$ на [0,1/2) та −1 на [1/2,1), і 0 всюди крім [0, 1). Для $n\geq 1$ запишемо $n=2^{j}+k,j\geq 0,0\leq k<2^{j}$ , і визначимо $h_{n}(x)=2^{j/2}h(2^{j}-k)$ . Носієм $h_{n}(x)$ буде інтервал $I_{n}=[k2^{-j},(k+1)2^{-j}]$ , що входить до [0, 1), коли $0\leq k\leq 2^{j}$ . Для завершення довизначимо $h_{0}(x)=1$ на [0, 1). Тепер побудований ряд $h_{0}(x),h_{1}(x),...,h_{n}(x),...$ це ортонормальний базис (іноді кажуть Гільбертів базис) в $L_{2}[0,1]$ . Апроксимація функції $f(x)$ послідовністю $S_{n}(f)(x)=<f,h_{0}>h_{0}(x)+...+<f,h_{n}>h_{n}(x)$ — це класична апроксимація неперервної функції.

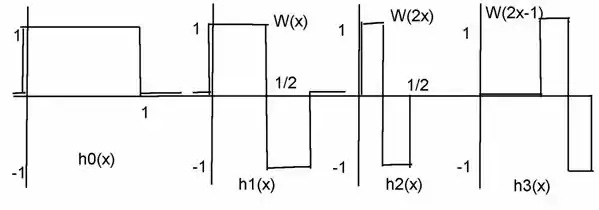Система функцій Хаара

Можна виділити дві основні операції над вихідною функцією: трансляція (зсув) та диляція (стискання, масштабування). 1) $W(2x)\rightarrow W(2x-1)$ 2) $W(x)\rightarrow W(2x)$ . На шляху до сучасних побудов теорії хвильок варто відзначити роботи радянського математика Лузіна (30-ті роки), які були продовжені Гвідо Вейссом (Guido Weiss) та Роналдом Куафманом (Ronald R. Coifman) у 60-ті — 80-ті. Їхній підхід використовувався для обробки сиґналів, і оснований на атомарних функціях. Сьогодні цей напрям розвивають учні В. Л. Рвачева (Харків). Вагомий внесок у теорію вейвлетів зробили Алекс Гроссманн і Жан Морле, які вперше вжили слово вейвлет і сформулювали те, що зараз відоме як CWT (1982). Вчені визначили вейвлет як набір функцій, породжених однією «материнською» функцією $\psi (x)$ . $\psi _{(a,b)}(x)=a^{-{\frac {n}{2}}}\psi ({\frac {x-b}{a}}),a>0,b\in R^{n}$ . Для функції $f(x)$ ці хвилькі $\psi _{(a,b)}$ відіграють роль ортонормованого базису, хвилькові коефіцієнти визначаються як $W(a,b)=<f,\psi _{(a,b))}>$ . Гроссманн та Морле дали наступне визначення: вейвлет це функція $\psi \in L_{2}(R^{n})$ , претворення Фур'є якої ${\bar {\psi }}(x)$ задовольняє умові $\int _{0}^{\infty }|{\bar {\psi }}(t\rho )|^{2}{\frac {dt}{t}}=1,\rho \in R^{n}$ майже всюди. Означення дискретних вейвлетів належить Штромберґу (Stromberg) та Мейєру (Y. Meyer) (1983). За ними вейвлет — це функція $\psi \in L_{2}(R^{n})$ , така, що $2^{\frac {j}{2}}\psi (2^{j}x-k),j,k\in Z$ утворює ортонормальний базис у $L_{2}$ .

Сучасний етап розвитку вейвлетів починається у 1985 з роботи Стефана Маллата (Stephane Mallat), спеціаліста з обробки зображень, в якій узагальнювалися вже існуючі теоретичні розробки: а) квадратурний дзеркальний фільтр (quadrature mirror filter) для цифрової телефонії; б) пірамідальний алгоритм Бурта-Аделсона (Burt Adelson), який використовувався для обробки зображень та в) ортонормальний вейвлет базис Штромберґа та Мейера. Маллат створив багаторозкладний аналіз (multiresolution analysis), який відкривав шлях до побудови теорії вейвлетів.

Найголовніший крок належить Інгрід Добеші (Ingrid Daubechies). У 1988 році вийшла її стаття, де вперше розглядається сімейство ортонормованих систем в $L_{2}$ з важливими особливостями:

кожна система породжується масштабною функцією $\phi (x)$ за допомогою трансляції та диляції;
кожен елемент даної системи має компактний носій і неперервний, або може бути вибраний досить гладкий (до певного порядку) шляхом зміни масштабу. Носії базисних функцій стають тим менші чим більший індекс j;
існують швидкі алгоритми для обчислень коефіцієнтів розкладу певної функції. Називається — дискретне вейвлет-перетворення від функції до вейвлет коефіцієнтів розкладу. Цей алгоритм має складність порядку O(N);
Класичне дискретне перетворення Фур'є та косинус перетворення з'являються як частинний випадок дискретного вейвлет-перетворення (DWT)
дискретне вейвлет-перетворення може бути розпаралелене.

Хвильки Добеші

Масштабна функція і відповідна хвилькова функція задовольняють

масштабному рівнянню (scaling equation) $\phi (x):=\sum _{k=0}^{2g-1}a_{k}\phi (2x-k)$ ;
відповідному хвильковому рівнянню (wavelet equation) $\psi (x):=\sum _{k=0}^{2g-1}b_{k}\phi (2x-k)$ ,

де коефіцієнти масштабного рівняння $a_{k}$ повинні задовольняти лінійній та квадратичній умовам $\sum a_{k}=2,\sum a_{k}a_{k+2l}=2\delta (l,0)$ , і де $b_{k}:=(-1)^{k+1}a_{2g-1-k}$ . Функції $\phi$ та $\psi$ задані на інтервалі [0, 2g-1] і утворюють трансляцією та диляцією вейвлет систему. Однією з властивостей технонології хвильок (вейвлет) є можливість вибрати систему коефіцієнтів, найбільш адаптовану до даної проблеми. Добеші у своїй роботі визначила сімейство хвилькових (вейвлет) систем, які мають максимальну кількість зникаючих моментів $\int x^{l}\psi (x)dx=0,l=0,...,g-1$ . Так коли $g=2$ можна явно знайти коефіцієнти $\{a_{n}\}_{n={\bar {o,3}}}$ : $\{{\frac {1+{\sqrt {3}}}{4}},{\frac {3+{\sqrt {3}}}{4}},{\frac {3-{\sqrt {3}}}{4}},{\frac {1-{\sqrt {3}}}{4}}\}$ . Задавати вейвлет систему можна різним чином. Поширення набуло таке задання $\phi _{k}(x):=\phi (x-k)$ , $\psi _{jk}(x):=2^{\frac {j}{2}}\psi (2^{j}x-k),j\geq 0$ . (Зазвичай система об'єднана з масштабними коефіцієнтами.) Вейвлет розвинення: $f(x)=\sum _{k}f_{k}\phi _{k}(x)+\sum _{j,k}f_{jk}\psi _{jk}(x)$ , де $f_{k}=\int f(x)\phi _{k}(x)dx$ , $f_{jk}=\int f(x)\psi _{jk}(x)dx$ .

Серед наступних робіт, які розвивали ідею вейвлетів Добеші виділяються праці Наталі Делпрат, яка надала часово-частотну інтерпретацію CWT (1991), Ньюланд, який розробив гармонійне вейвлет-перетворення та багато інших.

Зв'язки теорії вейвлетів

Теорія вейвлетів зв'язана з декількома іншими напрямами. Усі вейвлет-перетворення можуть розглядатися як різновид часово-частотного представлення і, отже відноситься до предмета гармонійного аналізу. Дискретне вейвлет-перетворення може розглядатися як різновид фільтра скінченної імпульсної відповіді. Вейвлети, що утворюють CWT підкоряються принципу невизначеності Гейзенберга і відповідно базис дискретного вейвлета також може розглядатися в контексті інших форм принципу невизначеності.

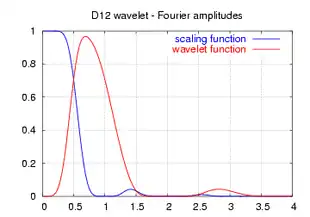
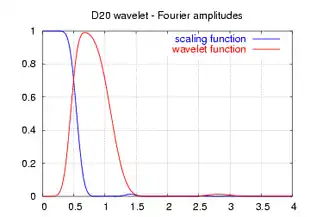
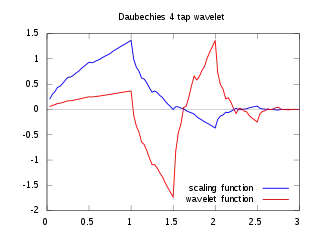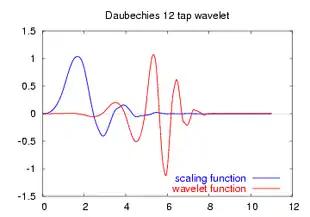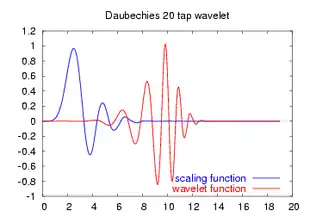скейлінг-функції $\phi$ і вейвлет $\psi$
амплітуда частотного спектру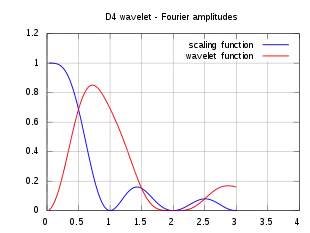

Література

Капшій О. В., Коваль О. І., Русин Б. П. Вейвлет-перетворення у компресії та попередній обробці зображень. — Львів : Сполом, 2008. — 206 с.
Блаттер К. Вейвлет-анализ. Основы теории. — М. : Техносфера, 2006. — 280 с.
Добеши И. Десять лекций по вейвлетам. — Ижевск : РХД, 2001. — 464 с.
Малла С. Вэйвлеты в обработке сигналов. — М. : Мир, 2005. — 672 с.
Смоленцев Н. К. Введение в теорию вейвлетов. — Ижевск : РХД, 2010. — 292 с.
Чуи К. Введение в вэйвлеты. — М. : Мир, 2001. — 412 с.

Посилання

Wavelet Digest Архівовано 29 вересня 2020 у Wayback Machine.
The Wavelet Tutorial by Polikar
[http://www.autex.spb.ru/cgi-bin/download.cgi?wvlt_tutorial%5Bнедоступне+посилання+з+березня+2019%5D Роби Поликар Введение в Вейвлет-преообразование]^{[недоступне посилання з жовтня 2019]} — 59 с. — Для тих, хто добре зрозумів ДПФ
J. Lewalle — Введение в анализ данных с применением непрерывного вейвлет-преобразования — 29 с. — Для тих, хто добре зрозумів роботу Робі Поликара «Введение в Вейвлет-преообразование»

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.