Графік Q-Q

Графік Q-Q використовується для порівняння форми розподілу, забезпечуючи графічне представлення про властивості, такі як місце розташування, масштаб та асиметрію у двох розподілів. Графік Q-Q може бути використана для порівняння набору даних, або теоретичного розподілу. Використання графіка Q-Q для порівняння двох наборів даних можна розглядати як непараметричний підхід до порівняння їх основних розподілів. Графік Q-Q — більш потужний підхід, ніж поширений метод порівняння гістограм двох зразків, але потребує більше вмінь щоб інтерпретувати. Графік Q-Q, як правило, використовуються для порівняння даних з теоретичною моделлю. Це може дати графічну оцінку. Графік Q-Q також використовуються для порівняння двох теоретичних розподілів. Оскільки графік Q-Q порівнює розподіли, то немає ніякої потреби в значення, які будуть спостерігатися у вигляді пар, як у діаграмі розсіювання, або навіть кількість значень у двох порівнюваних груп повинні бути рівні.

Термін «імовірнісний графік» іноді відноситься конкретно до графіка Q-Q, а іноді до більш загального класу діаграм, а іноді, рідше використовуються графік P-P. Коефіцієнту кореляції діаграми — це величина, що отримується з графіка Q-Q, яка вимірює відповідність розподілення з даними, що спостерігаються і яка іноді використовується як засіб встановлення розподілу даних.

Основним кроком у побудові графіка Q-Q — це розрахунок або оцінка квантилів, що повинні бути побудовані. Якщо одна або обидві осі в графіку Q-Q мають за основу теоретичний розподіл з неперервною функцією розподілу, всі квантилі однозначно визначені і можуть бути отримані шляхом використання неперервної функції розподілу. Якщо теоретичний розподіл ймовірностей з розривною неперервною функцією розподілу є однією з двох розподілів, які порівнюються, то деякі з квантилі не можуть бути визначені, так чином інтерпольований квантиль може бути нанесеним. Якщо графік Q-Q побудована на даних, існує кілька оцінок квантилів у використанні. Правила формування графіка Q-Q, коли квантиль повиннен бути оціненим або інтерпольованим, називають побудовою позицій.

Простий випадок, коли є два набори даних одного і того ж розміру. У цьому випадку, щоб побудувати графік Q-Q, кожен впорядковує кожний з двох наборів у порядку зростання, потім розділяє на пари відповідних значень. Більш складна конструкція це випадок, коли порівнюються два набори даних різних за розміром. Для побудови Q-Q графіка в цьому випадку необхідно використовувати інтерпольовану оцінку квантиля, так щоб квантиль відповідний до тієї ж базової ймовірності може бути побудованим.

Більш абстрактно, дано дві кумулятивні функції розподілу ймовірностей F та G, з пов'язананими функціями квантилів та (зворотня функція розподілу є функцією квантиля), графік Q-Q звертає квантиль F проти квантиля G для діапазону значень Q. Таким чином, графік Q-Q — це параметрична крива проіндексована більше ніж [0,1] зі значеннями в площині дійсних чисел.

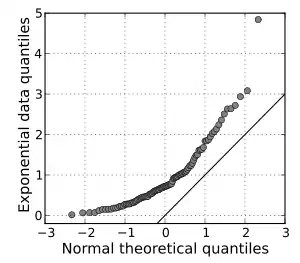
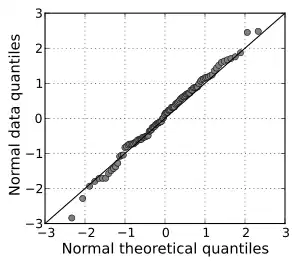
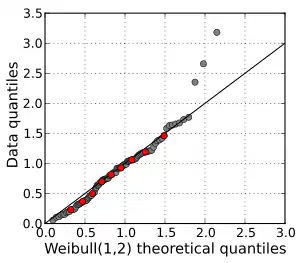
Точки графіку Q-Q завжди не спадають, якщо дивитися зліва направо. Якщо два порівнюваних розподілів ідентичні, графік Q-Q має вигляд лінії у = х. Якщо два розподіли узгоджені лінійно, то після перетворення значень в одному з розподілі Q-Q графік стане деякою лінією, але не обов'язково прямою у = х. Якщо загальна тенденція Q-Q графіку більш плоска, ніж пряма у = х, то розподіл нанесений на горизонтальну вісь більш розсіяний, ніж розподіл на вертикальній осі. І навпаки, якщо загальна тенденція Q-Q графіку крутіше лінії у = х, то розподіл на вертикальній осі більш розсіяний, ніж розподіл на горизонтальній осі. Q-Q графіки часто мають форму дуги або «S» форми, що показує, що однин з розподілів більш асиметричний, ніж інший, або, що один з розподілів має важчий хвіст, ніж інший.

Хоча Q-Q графік заснований на квантилях, в стандартному Q-Q графіку неможливо визначити, які точки в ньому визначає даний квантиль. Наприклад, неможливо визначити середнє значення будь-якого з двох розподілів, що порівнюються шляхом перевірки Q-Q графіка. Деякі Q-Q графіки вказують дециль для винесення рішень, якщо таке можливо.

Нахил і положення лінійної регресії між квантилями дає міру відносного місцезнаходження та відносної шкали зразків. Якщо медіани розподілу, які нанесені на горизонтальну вісь, дорівнюють 0, то перетин лінії регресії є мірою місцезнаходження, і нахил є мірою масштабу. Відстань між медіанами є ще одним заходом відносного розташування відображення в Q-Q графіку. «Імовірнісний графік коефіцієнта кореляції» — це коефіцієнт кореляції між парними квантилями зразка. Чим ближче коефіцієнт кореляції до одиниці, тим ближче розподіли знаходяться. Для розподілів з одним параметром форми, імовірнісний графік коефіцієнта кореляції забезпечує спосіб оцінки форми параметра — просто одна обчислює коефіцієнт кореляції для різних значень параметра форми, і використовує один з найбільш придатних, так якби порівнювали розподіли різних типів. Інший спосіб використання Q-Q графіків — це порівняння розподілу зразка до теоретичного розподілу, такі як стандартний нормальний розподіл N (0,1), як у нормальному графіку ймовірності.

Альтернативно, можна використовувати оцінки медіан порядкової статистики, які можна обчислити на основі оцінки середнього порядку рівномірного розподілу статистики та квантиль функції розподілу; це було запропоновано Філібеном в 1975.

Це може бути легко згенеровано для будь-якого розподілу, для яких квантиль функції можна обчислити, але, з іншої сторони, в результаті оцінки положення та масштабу вже не точними будуть оцінки найменших квадратів, хоча вони значно відрізняються тільки для малих.

Для квантилів розподілу порівняння зазвичай використовується формула k/(n + 1). Кілька різних формул були використані або запропоновані як симетрична побудова позицій. Такі формули мають вигляд (до — (k − a)/(n + 1 − 2a) при деякому значенні в діапазоні від 0 до 1/2, що дає діапазон між k/(n + 1) і (до — 1 / 2) / N. Інші вирази включають в себе:

• (k − 0.3) / (n + 0.4).
• (k − 0.3175) / (n + 0.365).
• (k − 0.326) / (n + 0.348).
• (k − ⅓) / (n + ⅓).
• (k − 0.375) / (n + 0.25).
• (k − 0.4) / (n + 0.2).
• (k − 0.44) / (n + 0.12).
• (k − 0.567) / (n − 0.134).
• (k − 1) / (n − 1).

Для великих розмірів вибірки, N, є невелика відмінність між цими різними виразами.

Медіани порядкової статистики є медіанами варіаційного розподілу. Вони можуть бути виражені через квантиль функцію та медіани порядкової статистики для неперервного рівномірного розподілу по:
${\displaystyle N(i)=G(U(i))}$
де U(i) — це однорідна медіана статистики та G — це квантиль функція для необхідного розподілу. Квантиль функція є зворотною до функції розподілу (ймовірність того, що X є меншим або рівним деякому значенню). Тобто, з урахуванням ймовірності, ми хочемо знайти відповідний квантиль інтегральної функції розподілу. Джеймс Дж. Філібен використовує наступні оцінки для однорідної медіани статистики:

${\displaystyle m(i)={\begin{cases}1-m(n)&i=1\\\\{\dfrac {i-0.3175}{n+0.365}}&i=2,3,\ldots ,n-1\\\\0.5^{1/n}&i=n.\end{cases}}}$

Обґрунтуванням такої оцінки є те, що медіана порядкової статистики не має просту форму.

• Графики квантиль-квантиль (Q-Q)