Граф Маꥳ

Граф МакЖі - це єдина (3,7) клітка (найменший кубічний з обхватом 7). Він є найменшою кубічної кліткою, яка не є графом Мура.

В теорії графів графом МакЖі, або (3-7)-клітиною, називається 3-регулярний граф з 24 вершинами і 36 ребрами[1]. Вперше відкритий Хорстом Саксом, але не опублікований[2][3], граф названий на честь МакЖі (англ. W. F. McGee), який опублікував результат в 1960 році. Пізніше, в 1966 році, Вільям Томас Татт довів, що це єдина (3,7)-клітина.

Відомі найменші кубічні графи з числом схрещувань 1-8 (послідовність A110507 в OEIS), найменший граф з числом схрещувань 8 - це граф МакГі. Існує 5 неізоморфних кубічних графів порядку 24 з числом схрещувань 8, один з них - узагальнений граф Петерсена G (12,5), відомий також як Граф Науру.

Граф МакГі має радіус 4, діаметр 4, хроматичної число 3 і хроматичний індекс 3. Він також 3-вершинно-зв'язний і 3-реберно-зв'язний.

Алгебраїчні властивості

Характеристичний многочлен графа МакЖі дорівнює .

Автоморфізм групи графа МакГі має порядок 32 і не транзитива щодо вершин - мається дві орбіти вершин довжини 8 і 16. Граф МакЖі - це найменша кубічна клітина, яка не є вершинно-транзитивною.

Галерея
  • Число переходів графа МакЖі дорівнює 8.
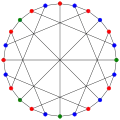  • Хроматичне число графа МакЖі дорівнює 3.
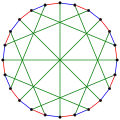  • Хроматичний індекс графа МакЖі дорівнює 3.
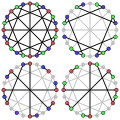  • The Ациклічний хроматичний індекс графа МакЖі равен 3.
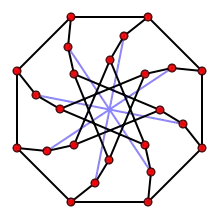  • Альтернативное изображение графа МакЖі.

Примітки
  1. http://mathworld.wolfram.com/GraphCrossingNumber.html
  2. Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
  3. McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.