Орбіта

У складі планетної системи, планети, карликові планети, астероїди та інші малі планети, комети й космічний пил рухаються по орбіті довкола барицентра системи еліптичними орбітами. Комети на параболічних або гіперболічних орбітах довкола барицентра гравітаційно не пов'язані із зорею і тому не розглядаються як частина планетної системи. Тіла, які гравітаційно пов'язані з однією з планет у планетній системі (природні або штучні супутники) рухаються по орбітах довкола барицентра відповідної планети.

Через взаємні гравітаційні пертурбації, ексцентриситети планетних орбіт змінюються з часом. Меркурій, найменша планета Сонячної Системи, має найбільш ексцентричну орбіту. У сучасну епоху, Марс має наступний за величиною ексцентриситет, у той час як найменші ексцентриситети орбіт мають Венера й Нептун.

Оскільки два об'єкти рухаються по орбітам довкола один одного, перицентром називають таку точку, в якій ці об'єкти перебувають один до одного найближче й апоцентром — точку, в якій вони найвіддаленіші один від одного. Для окремих тіл можуть використовуватися більш специфічні терміни. Наприклад, перигей і апогей — це найнижча й найвища точка орбіт довкола Землі, а перигелій і афелій є найближчою та найвіддаленішою точкою орбіти довкола Сонця.

У випадку, коли планети рухаються по орбіті довкола зорі, маса зорі і всіх її супутників враховуються для розрахунку однієї точки, яку називають барицентром. Траєкторіями руху всіх супутників зорі є еліптичні орбіти довкола барицентра. Кожен супутник у такій системі матиме свою еліптичну орбіту, в якій барицентр буде одним із фокусів еліпсу. На будь-якій точці орбіти, кожен супутник матиме певну величину кінетичної й потенційної енергії відносно барицентра, і його загальна енергія є постійною в кожній точці орбіти. У результаті, коли планета наближається до перицентра, вона буде збільшувати швидкість (оскільки її потенційна енергія зменшується); коли планета наближається до апоцентра, її швидкість зменшуватиметься (оскільки потенційна енергія збільшується).

Загальне пояснення

Існує два основних погляди на пояснення орбіт:

• Сила, така як сила тяжіння, змушує об'єкт рухатися вигнутою траєкторією при його спробі летіти по прямій лінії.
• Коли об'єкт притягується до масивного тіла, він падає в напрямку того тіла. Однак, якщо він має достатню тангенціальну швидкість, він не буде падати на інше тіло, а натомість буде продовжувати нескінченно слідувати вигнутою траєкторією, що викликає це тіло. Тоді говорять, що об'єкт обертається довкола небесного тіла.

Ньютонівська модель гарматного ядра, ілюстрація як об'єкти "падають" по кривій

Перетини конусів показують можливі орбіти (жовтим) невеликих об'єктів довкола Землі. Проекції цих орбіт на гравітаційний потенціал (синім) Землі дозволяє визначити орбітальну енергію в кожній точці у просторі.

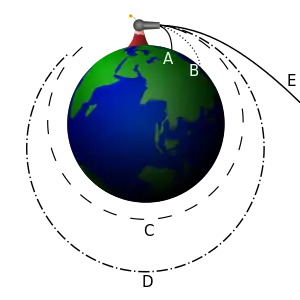
Для ілюстрації орбіти довкола планети є корисною Ньютонівська модель гарматного ядра (див. зображення). Це уявний експеримент, у якому деяка гармата на вершині високої гори здатна вистрілювати ядра горизонтально на будь-якій обраній швидкості. Дія сили тертя повітря на гарматне ядро не враховується (або ж вважається, що гора настільки висока, що гармата перебуває вище земної атмосфери, що приводить до того ж).[2]

Якщо гармата вистрілює ядро з малою початковою швидкістю, траєкторія ядра загинається вниз і ядро влучає в землю (A). Зі збільшенням швидкості, ядро падатиме на землю далі від гармати (B), оскільки хоч і ядро досі падає в напрямку землі, однак поверхня землі значно викривляється і стає далі від нього (дивись першу точку, зверху). У технічному розумінні всі ці рухи є «орбітами» – вони описують частину еліптичної траєкторії довкола центра мас – але орбіти перериваються влучанням у Землю.

Якщо гарматне ядро вистрілили з достатньою швидкістю, поверхня землі відхиляється від ядра настільки ж, наскільки падає ядро – тому ядро ніколи не досягне поверхні землі. Воно рухатиметься неперервною, або коловою орбітою як показано на прикладі (C). Для будь-якої комбінації висоти над центром мас і маси планети існує одна специфічна швидкість вистрілювання ядра. Вона не залежить від маси ядра, якщо вважати її дуже малою по відношенню до маси Землі.

Якщо швидкість вистрілювання збільшувати далі, утворюється неперервна еліптична орбіта, що позначена як (D). При вистрілюванні над поверхнею Землі, як показано, також утворюватимуться не перервані еліптичні орбіти і на меншій швидкості; вони пройдуть найближче до поверхні Землі у точці вищій ніж половина орбіти і прямо навпроти точки вистрілювання, під орбітою що обертається.

При певній горизонтальній швидкості вистрілювання, що називається другою космічною швидкістю, і залежить від маси планети, досягається відкрита орбіта (E), що має параболічну траєкторію. На ще більших швидкостях об'єкт рухатиметься по гіперболічних траєкторіях. У практичному розумінні, ці обидва типи траєкторій означають що об'єкт "відривається" від гравітації планети, і "вирушає у вільний космос" та ніколи не повернеться.

Деякий час вважалося, що планети Сонячної системи рухаються навколо Сонця коловими орбітами. Після довгих та невдалих спроб обчислити колову орбіту для Марса німецький астроном Йоганн Кеплер спростував це твердження та згодом, використовуючи дані вимірювань Тихо Браге, встановив закони руху планет навколо зорі, що тепер мають назву законів Кеплера:

1. Усі планети обертаються навколо Сонця орбітами, що мають форму еліпса, в одному з фокусів якого розташовано Сонце.
2. Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі.
3. Квадрат періоду обертання планети навколо Сонця прямо пропорційний кубу великої півосі еліпса.

Кеплерівські елементи орбіти:

• велика піввісь (англ. a) (або фокальний параметр)
• ексцентриситет (e)
• нахил орбіти (і) до основної координатної площини
• довгота висхідного вузла (Ω, node)
• аргумент перицентра (ω, peri)
• час проходження небесного тіла через перицентр (T0)

Ці елементи однозначно визначають орбіту незалежно від її форми (еліптичної, параболічної чи гіперболічної). Основною координатною площиною може бути площина екліптики, площина галактики, площина земного екватора тощо. У такому разі елементи орбіти задаються відносно обраної площини.