Граф Науру
У теорії графів, граф Науру — симетричний дводольний кубічний граф з 24 вершинами і 36 ребрами. Він був названий Девідом Епштейном на честь двадцятизіркового прапору Науру.[1]
| Nauru graph | |
|---|---|
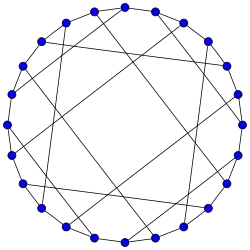 Граф Науру є Гамільтоновим графом. | |
| Вершин | 24 |
| Ребер | 36 |
| Радіус | 4 |
| Діаметр | 4 |
| Обхват | 6 |
| Автоморфізм | 144 (S4×S3) |
| Хроматичне число | 2 |
| Хроматичний індекс | 3 |
| Властивості |
Симетричний Кубічний Гамільтонів цілий Граф Келі Дводольний |
Його хроматичне число — 2, хроматичний індекс — 3, діаметр — 4, радіус — 4 та обхват — 6.[2] Він так само містить 3-вершинно-зв'язний та 3-реберно-зв'язний графи.
Найменші кубічні графи з числами схрещувань 1-8 відомі (послідовність A110507 з Онлайн енциклопедії послідовностей цілих чисел, OEIS). Найменший граф з числом схрещувань 8 — граф Науру. Існує 5 неізоморфних кубічних графів 24-го порядку з числом перетину 8.[3] Один з них являє собою граф Маꥳ, також відомий як (3-7)-клітина.[4]
Конструкція
Граф Науру це Гамільтонів граф, він може бути описаний LCF-нотацією: [5, −9, 7, 9, −7, −5]4.[1]
Граф Науру може бути побудований як узагальнений граф Петерсена G (12, 5), який утворюється на вершинах дванадцятикутника, пов'язаних з вершинами дванадцяти-кінцевої зірки, в якій кожна точка зірки поєднується точками за п'ять кроків від нього.
Така можлива комбінаторна побудова графу Науру. Візьміть три неоднакові об'єкти і розмістіть їх у чотири неоднакові коробки, не більше одного об'єкта в коробці. Є 24 способи, щоб розподілити об'єкти, відповідно 24 вершинам графу. Якщо можливо перейти з одного положення в інше, переміщуючи рівно один об'єкт із його поточного місця розташування у порожнє місце, то вершини, що відповідають двом положенням, поєднуються ребром. Як результат, графом переходу станів є граф Науру.
Алгебраїчні властивості
Група автоморфізмів графу Науру — група порядку 144.[5] Вона ізоморфна прямому добутку симетричних груп S4 і S3 і діє транзитивно на вершинах по краях і на дугах графу. Тому графік Науру — симетричний граф. Він має автоморфізми, які переміщують будь-яку вершину до будь-якої іншої вершини і будь-яке ребро до будь-якого іншого ребра. За даними перепису Фостера, граф Науру є єдиним кубічно-симетричним графом на 24 вершинах.[2]
Узагальнений граф Петерсена G(n, k) є вершинно-транзитивним тоді, і тільки тоді, коли n = 10 і k = 2 або якщо k2 ≡ ± 1 (mod n) і є реберно-транзитивним тільки в наступних випадках: (n, k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5).[6] Таким чином, граф Науру є одним з семи симетричних узагальнених графів Петерсена. Серед цих семи графів кубічний граф , граф Петерсена , граф Мебіуса — Кантора , додекаедрічний граф і граф Дезарга .
Граф Науру — це граф Келі групи S4, симетричної групи перестановок чотирьох елементів, що породжується трьома різними способами перестановки першого елементу з трьома іншими: (1 2), (1 3) і (1 4).
Характеристичний поліном графу Науру дорівнює
що робить його цілим графом, тобто графом спектр якого складається повністю з цілих чисел.

.svg.png.webp) Симетричний тор . Тор формується, топологічно, склеюванням протилежних країв правильного шестикутника один до одного. |
.svg.png.webp) |
.svg.png.webp) Матриця суміжності.
Кожне ребро представляє два записи однакового кольору, що є симетричними до головної діагоналі. |
Топологічні властивості
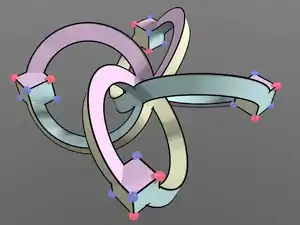
Граф Науру має два різних вкладення у вигляді узагальнених правильних багатогранників: топологічні поверхні розбиваються на ряд ребер, вершин і граней таким чином, що існує симетричний перекид будь-якого прапорця (інцидентна трійка з вершини, ребра та грані) у будь-який інший прапорець.[7]
Одне з цих двох вкладень утворює тор, тому граф Науру — це тороїдальний граф: він складається з 12 шестикутних граней разом з 24 вершинами і 36 ребрами графу Науру. Двоїстий граф — це вкладення симетричного 6-регулярного графу з 12 вершинами і 36 ребрами.
Інші симетричні вкладення графу Науру мають шість дванадцятикутних граней, які утворюють поверхню 4 роду . Двоїстий граф може бути сформований з простого графу.
Геометричні властивості
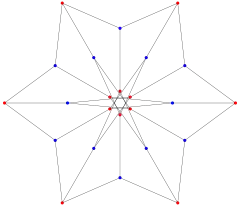
Як і у всіх узагальнених графах Петерсена, граф Науру можна представити точками на площині таким чином, що сусідні вершини знаходяться на одиниці відстані один від одного. Це граф одиничної відстані.[8] Такими є тільки узагальнені графи Петерсена G (n, р), вони не можуть бути представлені таким чином, що симетрії малюнка утворюють циклічну групу порядку n. Замість цього, одинична відстань графу має діедральну групу Dih6 як групу її симетрії.
Історія
Першою людиною, що написала про граф Науру був Рональд Фостер, він зробив це у спробі зібрати усі кубічні симетричні графи.[9] Список кубічних симетричних графів зараз носить ім'я Перепис Фостера і всередині цього списку граф Науру має номер F24A, але не має конкретного імені.[10] У 1950 р. Гарольд Коксетер описав граф у другий раз, даючи ствердження Гамільтона для ілюстрації цієї статті, та описуючи його як граф Леві проєктивної конфігурації, описаного Захарієм.[11][12]
У 2003, Ед Пегг написав у своєму онлайн-МАА рубрику про те, що F24A заслуговує на назву, але не запропонував її.[13] Нарешті, у 2007 році, Девід Епштейн використав ім'я Граф Науру, тому що прапор Республіки Науру має 12-кінцеву зірку, аналогічну до тієї, що з'являється в конструкції графу як узагальнений граф Петерсена.[1]
Примітки
- Eppstein, D., The many faces of the Nauru graph Архівовано 21 липня 2011 у Wayback Machine. on LiveJournal, 2007.
- Conder, M. and Dobcsányi, P. «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
- Pegg, E. T.; Exoo, G. (2009). Crossing number graphs. Mathematica Journal 11..
- Weisstein, Eric W. Graph Crossing Number(англ.) на сайті Wolfram MathWorld.
- Royle, G. F024A data Архівовано 6 березня 2011 у Wayback Machine.
- Frucht, R.; Graver, J. E.; Watkins, M. E. (1971). The groups of the generalized Petersen graphs. Proceedings of the Cambridge Philosophical Society 70: 211–218. doi:10.1017/S0305004100049811..
- McMullen, Peter (1992). The regular polyhedra of type {p, 3} with 2p vertices. Geometriae Dedicata 43 (3): 285–289. doi:10.1007/BF00151518..
- Žitnik, Arjana; Horvat, Boris; Pisanski, Tomaž (2010). All generalized Petersen graphs are unit-distance graphs. IMFM preprints 1109..
- Foster, R. M. (1932). Geometrical circuits of electrical networks. Transactions of the American Institute of Electrical Engineers 51: 309–317. doi:10.1109/T-AIEE.1932.5056068..
- Bouwer, I. Z.; Chernoff, W. W.; Monson, B.; Star, Z (1988). The Foster Census. Charles Babbage Research Centre..
- Coxeter, H. S. M. (1950). Self-dual configurations and regular graphs. Bulletin of the American Mathematical Society 56: 413–455. doi:10.1090/S0002-9904-1950-09407-5..
- Zacharias, M. (1941). Untersuchungen über ebene Konfigurationen (124, 163). Deutsche Mathematik 6: 147–170..
- Pegg, Ed (2003). Cubic Symmetric Graphs. Mathematical Association of America..