Граф Мура

Граф Петерсена як граф Мура. Будь-яке дерево пошуку в ширину має ${\displaystyle d(d-1)^{i}}$ вершин у його i-ому рівні.

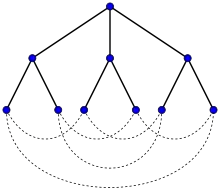
Нехай ${\displaystyle G}$ — будь-який граф із найбільшим степенем ${\displaystyle d}$ і діаметром ${\displaystyle k}$, тоді візьмемо дерево, утворене пошуком у ширину, з коренем у вершині ${\displaystyle v}$. Це дерево має 1 вершину рівня 0 (сама вершина ${\displaystyle v}$), і максимум ${\displaystyle d}$ вершин рівня 1 (сусіди вершини ${\displaystyle v}$). На наступному рівні є максимум ${\displaystyle d(d-1)}$ вершин — кожен сусід вершини ${\displaystyle v}$ використовує одне ребро для з'єднання з вершиною ${\displaystyle v}$, так що має максимум ${\displaystyle d-1}$ сусідів рівня 2. У загальному випадку подібні доводи показують, що на будь-якому рівні ${\displaystyle 1\leq {i}\leq {k}}$ може бути не більше ${\displaystyle d(d-1)^{i}}$ вершин. Таким чином, загальне число вершин може бути не більшим від

${\displaystyle 1+d\sum _{i=0}^{k-1}(d-1)^{i}.}$

Гоффман і Сінглтон[2] спочатку визначили граф Мура як граф, для якого ця межа числа вершин досягається. Таким чином, будь-який граф Мура має максимально можливе число вершин серед усіх графів, у яких степінь не перевершує ${\displaystyle d}$, а діаметр — ${\displaystyle k}$.

Пізніше Сінглтон[4] показав, що графи Мура можна еквівалентно визначити як граф, що має діаметр ${\displaystyle k}$ і обхват ${\displaystyle 2k-1}$. Ці дві вимоги комбінуються, з чого виводиться d-регулярність графа для деякого ${\displaystyle d}$.

Замість верхньої межі числа вершин у графі в термінах його найбільшого степеня і діаметра ми можемо використовувати нижню межу числа вершин у термінах найменшого степеня і обхвату[3]. Припустимо, що граф ${\displaystyle G}$ має найменший степінь ${\displaystyle d}$ і обхват ${\displaystyle 2k+1}$. Виберемо довільну початкову вершину ${\displaystyle v}$ і, як і раніше, уявимо дерево пошуку в ширину з коренем у ${\displaystyle v}$. Це дерево повинне мати одну вершину рівня 0 (сама вершина ${\displaystyle v}$) і щонайменше ${\displaystyle d}$ вершин на рівні 1. На рівні 2 (для ${\displaystyle k>1}$), має бути щонайменше ${\displaystyle d(d-1)}$ вершин, оскільки кожна вершина на рівні ${\displaystyle l}$ має щонайменше ще ${\displaystyle d-1}$ зв'язків, і ніякі дві вершини рівня 1 не можуть бути суміжними або мати спільні вершини рівня 2, оскільки утворився б цикл, коротший, ніж обхват. У загальному випадку схожі доводи показують, що на будь-якому рівні ${\displaystyle 1\leq {i}\leq {k}}$ має бути принаймні ${\displaystyle d(d-1)^{i}}$ вершин. Таким чином, загальне число вершин має бути не менше від

${\displaystyle 1+d\sum _{i=0}^{k-1}(d-1)^{i}.}$

У графі Мура це число вершин досягається. Кожен граф Мура має обхват рівно ${\displaystyle 2k+1}$ — він не має достатньо вершин, щоб мати більший обхват, а коротший цикл призвів би до нестачі вершин на перших ${\displaystyle k}$ рівнях деяких дерев пошуку в ширину. Таким чином, будь-який граф Мура має мінімально можливе число вершин серед усіх графів з мінімальним степенем ${\displaystyle d}$ і діаметром ${\displaystyle k}$ — він є кліткою.

Для парного обхвату ${\displaystyle 2k}$ можна утворити аналогічне дерево пошуку в ширину, починаючи зі середини одного ребра. Отримуємо межу мінімального числа вершин у графі цього обхвату з мінімальним степенем ${\displaystyle d}$

${\displaystyle 2\sum _{i=0}^{k-1}(d-1)^{i}=1+(d-1)^{k-1}+d\sum _{i=0}^{k-2}(d-1)^{i}.}$

Таким чином, до графів Мура іноді відносять графи, на яких ця межа досягається. Знову ж, будь-який такий граф є кліткою.

Теорема Гоффмана — Сінглтона стверджує, що будь-який граф Мура з обхватом 5 повинен мати степінь 2, 3, 7 або 57. Графами Мура є:

• Повні графи ${\displaystyle K_{n}}$ з N > 2 вершинами (діаметр 1, обхват 3, степінь n-1, порядок ${\displaystyle n}$).
• Непарний цикл ${\displaystyle C_{2n+1}}$ (діаметр ${\displaystyle n}$, обхват ${\displaystyle 2n+1}$, степінь 2, порядок 2n+1).
• Граф Петерсена (діаметр 2, обхват 5, степінь 3, порядок 10).
• Граф Гоффмана-Сінглтона (діаметр 2, обхват 5, степінь 7, порядок 50).
• Гіпотетичний граф з діаметром 2, обхватом 5, степенем 57 і порядком 3250, нині невідомо, чи такий існує.

Хіґман показав, що, на відміну від інших графів Мура, невідомий граф не може бути вершинно-транзитивним. Мачай і Ширан пізніше показали, що порядок автоморфізмів такого графа не перевищує 375.

В узагальненому визначенні графів Мура, де дозволяється парний обхват, графи з парним обхватом відповідають графам інцидентності (можливо вироджених) узагальнених багатокутників. Кілька прикладів — парні цикли ${\displaystyle C_{2n}}$, повні дводольні графи ${\displaystyle K_{n,n}}$ з обхватом чотири, граф Хівуда зі степенем 3 і обхватом 6 і граф Татта — Коксетера зі степенем 3 і обхватом 8. Відомо[5][6], що всі графи Мура, крім перерахованих вище, повинні мати обхват 5, 6, 8 або 12. Випадок парного обхвату випливає з теореми Фейта — Хіґмана про можливі значення ${\displaystyle n}$ для узагальнених n-кутників.

• Проблема розміру — діаметра
• Таблиця найбільших відомих графів для заданого діаметра і максимального степеня

• Jernej Azarija, Sandi Klavžar. Moore Graphs and Cycles Are Extremal Graphs for Convex Cycles // Journal of Graph Theory. — 2015. — Т. 80 (3 лютого). — С. 34–42. — DOI:10.1002/jgt.21837.
• Béla Bollobás. Modern graph theory. — Springer-Verlag, 1998. — Т. 184. — (Graduate Texts in Mathematics).
• E. Bannai, T. Ito. On finite Moore graphs // Journal of the Faculty of Science, the University of Tokyo. Sect. 1 A, Mathematics. — 1973. — Т. 20 (3 лютого). — С. 191–208. Архівовано з джерела 24 квітня 2012.
• R. M. Damerell. On Moore graphs // Mathematical Proceedings of the Cambridge Philosophical Society. — 1973. — Т. 74 (3 лютого). — С. 227–236. — DOI:10.1017/S0305004100048015.
• Paul Erdős, Alfréd Rényi, Vera T. Sós. On a problem of graph theory // Studia Sci. Math. Hungar.. — 1966. — Т. 1 (3 лютого). — С. 215–235..
• Alan J. Hoffman, Robert R. Singleton. Moore graphs with diameter 2 and 3 // IBM Journal of Research and Development. — 1960. — Т. 5, вип. 4 (3 лютого). — С. 497–504. — DOI:10.1147/rd.45.0497.
• Martin Mačaj, Jozef Širáň. Search for properties of the missing Moore graph // Linear Algebra and its Applications. — 2010. — Т. 432 (3 лютого). — С. 2381–2398. — DOI:10.1016/j.laa.2009.07.018..
• Robert R. Singleton. There is no irregular Moore graph // American Mathematical Monthly. — 1968. — Т. 75, вип. 1 (3 лютого). — С. 42–43. — DOI:10.2307/2315106.

• Андріс Браувер і Віллем Гемерс (Willem H. Haemers): Spectra of graphs
• Weisstein, Eric W. Граф Мура(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Теорема Гоффмана — Сінглтона(англ.) на сайті Wolfram MathWorld.