Групи Томпсона

${\displaystyle F(p)}$ є природним узагальненням ${\displaystyle F}$ і зберігає чимало її властивостей. Для ${\displaystyle F=F(2)}$ існує скінченне задання:

${\displaystyle F=F(2)=\langle A,B\mid \ [AB^{-1},A^{-1}BA]=[AB^{-1},A^{-2}BA^{2}]=\mathrm {id} \rangle }$

де ${\displaystyle \left[x,y\right]}$ є комутатором, тобто ${\displaystyle xyx^{-1}y^{-1}}$.

Узагальнивши для ${\displaystyle F(p)}$, матимемо ${\displaystyle p}$ твірних ${\displaystyle x_{0},x_{1},x_{2},\dots \ ,x_{p-1}}$ і ${\displaystyle p(p-1)}$ визначальних співвідношень.

${\displaystyle F(p)}$ можемо також задати як:

${\displaystyle F(p)=\langle x_{0},x_{1},x_{2},\dots \ \mid \ x_{k}^{-1}x_{n}x_{k}=x_{n+p-1}\ \mathrm {,} \ k<n\rangle .}$

При ${\displaystyle F=F(2)}$ очевидно матимемо:

${\displaystyle F=F(2)=\langle x_{0},x_{1},x_{2},\dots \ \mid \ x_{k}^{-1}x_{n}x_{k}=x_{n+1}\ \mathrm {,} \ k<n\rangle .}$

Нескінченне задання ${\displaystyle F(2)}$ пов'язане зі скінченним як ${\displaystyle x_{0}=A,x_{n}=A^{1-n}BA^{n-1}}$ для ${\displaystyle n>0}$. Аби визначити метрику слів (або ж довжину елемента) користатимемось саме скінченним представленням.

Зі співвідношення ${\displaystyle x_{k}^{-1}x_{n}x_{k}=x_{n+p-1}}$ можемо отримати, що довільний елемент ${\displaystyle F(p)}$ подається в нормальній формі (НФ):

${\displaystyle x_{k_{1}}^{r_{1}}x_{k_{2}}^{r_{2}}\dots x_{k_{i}}^{r_{i}}x_{n_{j}}^{-s_{j}}\dots x_{n_{2}}^{-s_{2}}x_{n_{1}}^{-s_{1}}}$ , де ${\displaystyle \ k_{1}<k_{2}<\dots <k_{n}\neq n_{j}>\dots >n_{2}>n_{1}}$

Покажімо коректність для ${\displaystyle F(2)}$. Перетворивши визначальне співвідношення, маємо

(1) ${\displaystyle x_{n}x_{k}=x_{k}x_{n+1}}$ та

(2) ${\displaystyle x_{k}^{-1}x_{n}=x_{n+1}x_{k}^{-1}}$

(1) гарантує, що ми завжди можемо впорядкувати ${\displaystyle x_{k}}$-ті за зростанням чи спаданням індексу (залежно від того, в якій частині розкладу ми знаходимось). (2) забезпечує обмінювання додатнього елемента і від'ємного, тим самим відсортовуючи всі додатні елементи в лівій частині, а від'ємні — в правій частині НФ.

Таке представлення буде єдиним, якщо накладемо додаткову вимогу:

щойно в розкладі елемента трапляються і ${\displaystyle x_{i}}$, і ${\displaystyle x_{i}^{-1}}$, то має бути ${\displaystyle x_{i+1}}$ або ${\displaystyle x_{i+1}^{-1}}$

Оскільки інакше, завдяки (2) ми виконуватимемо обміннювання елементів ${\displaystyle x_{i}}$ і ${\displaystyle x_{i}^{-1}}$ з сусідніми, наближаючи їх один до одного доти, доки вони не стоятимуть поруч, і ми зможемо скоротити.

Група F(p) дає змогу визначити зсув ${\displaystyle \phi }$, який переводить ${\displaystyle x_{i}}$ в ${\displaystyle x_{i+1}}$. Такий зсув задовільняє умові ${\displaystyle x_{0}^{-1}\phi (x)x_{0}=\phi ^{p}(x)}$ для всіх ${\displaystyle x\in F(p)}$.

Томпсонова група F породжується подібними операціями над двійковими деревами. Тут L і T є вузлами, а A, B і R можуть бути замінені більш розгалуженими деревами.

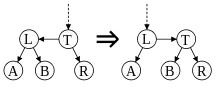
Група F також зображується з погляду операцій на впорядкованих кореневих двійкових деревах, або як група шматковолінійних гомеоморфізмів одиничного відрізка, що зберігають орієнтацію, недиференційовні крапки мають диадичні координати і всі похідні є ступенями двійки.

Група F може також розглядатися як дія на одиничному колі, визначаючись двома кінцевими точками одиничного відрізка, а група T як група автоморфізмів кола, отриманих шляхом додавання гомеоморфізму x→x +1/2 mod 1 до F. У двійкових деревах це відповідає перестановці двох дерев під коренем. Група V отримується з Т додаванням розривного відображення, яке діє незмінним чином на напівінтервалі [0,1/2) та обмінює [1/2,3/4) і [3/4,1). У двійкових деревах це відповідає обміну двох піддерев під правим нащадком кореня (якщо він існує).

• Група Гіґмана

• Cannon, J. W.; Floyd, W. J.; Parry, W. R. (1996). Introductory notes on Richard Thompson's groups (PDF). L'Enseignement Mathématique. Revue Internationale. IIe Série 42 (3): 215–256. ISSN 0013-8584. MR 1426438.
• Cannon, J.W.; Floyd, W.J. (September 2011). WHAT IS...Thompson's Group? (PDF). Notices of the American Mathematical Society 58 (8): 1112–1113. ISSN 0002-9920. Процитовано 27 грудня 2011.
• Higman, Graham (1974). Finitely presented infinite simple groups. Notes on Pure Mathematics 8. Department of Pure Mathematics, Department of Mathematics, I.A.S. Australian National University, Canberra. ISBN 978-0-7081-0300-5. MR0376874.
• Metrics and embeddings of generalizations of Thompson's group F. Автори: J. Burillo; S. Cleary; M. I. Stein Journal: Trans. Amer. Math. Soc. 353 (2001)
• Introduction to Thompson's Group F — Daniel Yeow