Гіпотеза Андріци

На початку 2000-х років з використанням даних про найбільші інтервали простих чисел гіпотезу перевірено аж до ${\displaystyle 1{,}3002\times 10^{16}}$[2]. Використовуючи таблицю максимальних інтервалів і нерівність для інтервалів, можна розширити значення підтвердження аж до ${\displaystyle 4\times 10^{18}}$.

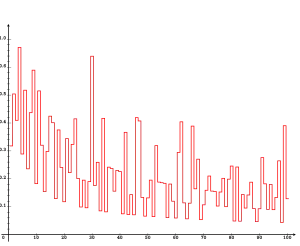
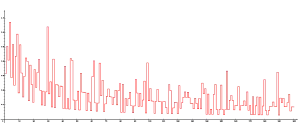
Існує графічна ілюстрація гіпотези: для дискретної функції ${\displaystyle A_{n}={\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}}$ (функції Андріци) найбільше значення спостерігається в точці ${\displaystyle n=4}$ зі значенням ${\displaystyle A_{4}\approx 0{,}670873\dots }$, і більших значень немає серед перших 10⁵ простих чисел. Оскільки функція Андріци асимптотично спадає в міру зростання ${\displaystyle n}$, гіпотеза з великою ймовірністю правильна, але залишається недоведеною.

Як узагальнення гіпотези Андріци розглядається така рівність:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}=1,}$

де ${\displaystyle p_{n}}$ — ${\displaystyle n}$-е просте, а ${\displaystyle x}$ може бути будь-яким додатним (дійсним) числом.

Найбільший можливий розв'язок за ${\displaystyle x}$ знаходиться при ${\displaystyle n=1}$, коли ${\displaystyle x_{\max }=1}$. Є гіпотеза, що найменше значення ${\displaystyle x}$ дорівнює ${\displaystyle x_{\min }\approx 0{,}567148\dots }$, яке знаходиться при ${\displaystyle n=30}$.

Ця гіпотеза формулюється у вигляді нерівності, яка узагальнює гіпотезу Андріци:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}<1}$ для ${\displaystyle x<x_{\min }}$.

• Гіпотеза Крамера
• Гіпотеза Лежандра
• Гіпотеза Фірузбехта

• Richard K. Guy. Unsolved problems in number theory. — 3rd. — Springer-Verlag, 2004. — ISBN 978-0-387-20860-2.
• Andrica D. Note on a conjecture in prime number theory // Studia Univ. Babes–Bolyai Math.. — 1986. — Т. 31, № 4. — С. 44–48. — ISSN 0252-1938.
• Prime Numbers: The Most Mysterious Figures in Math. — John Wiley & Sons, Inc., 2005. — ISBN 0-471-46234-9.

• Andrica 's Conjecture на PlanetMath
• Generalized Andrica conjecture на PlanetMath
• Weisstein, Eric W. Andrica's Conjecture(англ.) на сайті Wolfram MathWorld.