Гіпотеза Крамера

Гіпотеза Крамера ґрунтується на ймовірнісній моделі (істотно евристичній) розподілу простих чисел, в якій передбачається, що ймовірність того, що натуральне число x є простим, дорівнює приблизно ${\displaystyle {\frac {1}{\ln x}}}$. Ця модель відома як Модель простих Крамера. Крамер довів у своїй моделі, що згадана гіпотеза істинна з імовірністю 1.[1]

Крамер також дав умовний доказ слабшого твердження про те, що

${\displaystyle p_{n+1}-p_{n}=O({\sqrt {p_{n}}}\ln p_{n})}$

припускаючи істинною гіпотезу Рімана.[1]

З іншого боку, E. Westzynthius довів в 1931 році, що величина пробілів між простими більша, ніж логарифмічна. Тобто,[2]

${\displaystyle \limsup _{n\to +\infty }{\frac {p_{n+1}-p_{n}}{\ln p_{n}}}=\infty .}$

Функція прогалин між простими числами

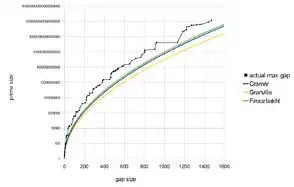
Даніель Шенкс запропонував гіпотезу про асимптотичну рівність для найбільших прогалин між простими, дещо більш сильну, ніж гіпотеза Крамера.[3]

У ймовірнісній моделі,

${\displaystyle \limsup _{n\rightarrow \infty }{\frac {p_{n+1}-p_{n}}{\ln ^{2}p_{n}}}=c,}$ де ${\displaystyle c=1.}$

Але константа ${\displaystyle c}$ можливо не така, як для простих, за теоремою Маєра. Ендрю Гренвіль в 1995 році стверджував, що константа ${\displaystyle c=2e^{-\gamma }\approx 1.1229\ldots .}$[4], де ${\displaystyle \gamma }$ — Стала Ейлера—Маскероні.

В праці[5] М. Вольф запропонував формулу для максимальної відстані ${\displaystyle G(x)}$ між подальшими прямими числами меншими за ${\displaystyle x}$, що виражена через функцію розподілу простих чисел ${\displaystyle \pi (x)}$:

${\displaystyle G(x)\sim {\frac {x}{\pi (x)}}(2\ln(\pi (x))-\ln(x)+c_{0}),}$

де ${\displaystyle c_{0}=\ln(C_{2})=0.2778769...}$, а ${\displaystyle C_{2}=1.3203236...}$ є константа простих-близнюків.

Томас Найслі обчислив багато найбільших прогалин між простими.[6] Він перевірив якість гіпотези Крамера, вимірявши частку R логарифма простих до квадратного кореня розміру прогалини між простими; він писав, «Для найбільших відомих прогалин, R залишається рівним приблизно 1,13», що показує, як мінімум в діапазоні його обчислень, що гренвіллево поліпшення гіпотези Крамера бачиться як найкраще наближення для даних.

• Теорема про розподіл простих чисел
• Проміжки між простими числами

• Weisstein, Eric W. Cramér Conjecture(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Cramér-Granville Conjecture(англ.) на сайті Wolfram MathWorld.