Гіпотеза Коллатца

Гіпотеза Коллатца (гіпотеза 3n+1, гіпотеза 3x+1, проблема Коллатца, проблема 3n+1, проблема 3x+1, Сіракузька проблема) — одна з нерозв'язаних проблем математики, названа на честь німецького математика Лотара Коллатца, який запропонував її у 1937 році.

Сіракузька послідовність

Для пояснення суті гіпотези розглянемо наступну послідовність чисел, яка називається Сіракузькою послідовністю. Беремо будь-яке натуральне число n. Якщо воно парне, то ділимо його на 2, а якщо непарне, то множимо на 3 і додаємо 1 (отримуємо 3n + 1). Над отриманим числом виконуємо ті ж самі дії, і так далі.

Графік послідовності для числа 27

Наприклад, для числа 3 отримуємо:

3 — непарне, 3 × 3 + 1 = 10
10 — парне, 10:2 = 5
5 — непарне, 5 × 3 + 1 = 16
16 — парне, 16:2 = 8
8 — парне, 8:2 = 4
4 — парне, 4:2 = 2
2 — парне, 2:2 = 1
1 — непарне, 1 × 3 + 1 = 4

Очевидно, що, починаючи з 1, починають циклічно повторюватися числа 1, 4, 2.

Для числа 27 маємо : 27, 82, 41, 124 , 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, …

Послідовність прийшла до одиниці тільки через 111 кроків, досягнувши пікового значення 9232.

Гіпотеза Коллатца полягає в тому, що яке б початкове число ми не взяли, рано чи пізно ми отримаємо одиницю.

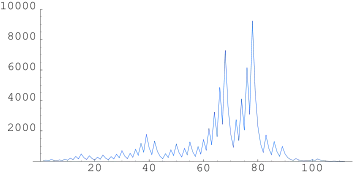
Числа — градини — також поширена назва для сукупності розглянутих послідовностей. Така назва виникла через те, що графіки послідовностей (див. ілюстрацію) схожі на траєкторію руху градин в атмосфері.

Проект «Collatz Conjecture»

У серпні 2009 року на платформі BOINC був запущений проект добровільних розподілених обчислень «Collatz Conjecture», метою якого є перевірка гіпотези Коллатца на великих числах. Обчислювальний модуль проекту може використовувати обчислювальні потужності сучасних відеокарт для одночасної обробки і вирахування послідовностей.

Візуалізація
  • Напрямлений граф, що показує орбіти невеликих чисел при відображенні карти Коллатца.
  • Напрямлений граф, що показує орбіти перших 1000 номерів.
  • х — стартовий номер
    у — найбільше число в ланцюгу на шляху до 1.

Аргументи на користь теорії

Хоча гіпотеза не була доведена, більшість математиків, які розглядали цю проблему, вважають гіпотезу істинною, тому що експериментальні дані і евристичні міркування підтримують її.

Ймовірнісний підхід

Якщо врахувати, тільки непарні числа в послідовності, породженій процесом Коллатц, то кожне непарне число складає в середньому 3/4 попереднього. З цього витікає евристичний аргумент, що будь-яка послідовність чисел-градин повинна зменшуватись в довгостроковій перспективі, хоча це не є аргументом проти інших циклів, тільки проти дивергенції. Аргумент не є доказом, оскільки він припускає, що послідовності градини збираються з некорельованих ймовірнісних подій.

Суворі обмеження

Хоча достеменно не відомо чи всі додатні числа в кінцевому підсумку зводяться до одиниці відповідно до гіпотези Коллатца, відомо, що багато чисел дійсно зводяться. Зокрема, Красиков і Лагарис довели, що кількість цілих чисел в інтервалі [1, х], що в кінцевому підсумку зводяться до одиниці, принаймні пропорційна x0.84.

Див. також

Література
  • Хейєс, Браян. Злети та падіння чисел-градин // В світі науки (Scientific American, видання російською мовою). — 1984. — № 3. — С. 102–107.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.