Дилогарифм
Дилогарифм — спеціальна функція в математиці, яка позначається і є окремим випадком полілогарифма при . Дилогарифм визначається як
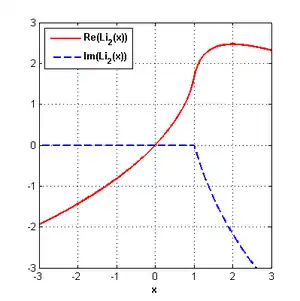
Наведене визначення дилогарифма правильне для комплексних значень змінної z. Для дійсних значень z = x у цій функції є розріз уздовж дійсної осі від 1 до . Зазвичай значення функції на розрізі визначається так, що уявна частина ділогарифма від'ємна:
Функцію часто називають дилогарифмом Ейлера, на честь Леонарда Ейлера, який розглянув її 1768 року[1]. Іноді дилогарифм називають функцією Спенса (англ. Spence's function) або інтегралом Спенса[2] на честь шотландського математика Вільяма Спенса (William Spence, 1777—1815)[3], який на початку XIX століття досліджував функції, відповідні і . Назву «дилогарифм» увів Гілл (C.J. Hill) 1828 року.
Функціональні співвідношення
Для дилогарифма існує низка корисних функціональних співвідношень,
для дійсних ,
Відомі також співвідношення, що містять дві незалежні змінні — наприклад, тотожність Гілла:
Окремі значення
Використовуючи співвідношення між функціями від x і 1/x, отримуємо
Існує також низка результатів для аргументів, пов'язаних з золотим перетином ,
а також для дилогарифма уявного аргументу,
де G — стала Каталана.
Співвідношення для окремих значень
Функції, пов'язані з дилогарифмом
- Функція Клаузена
- Виникає при розгляді дилогарифма, аргумент якого знаходиться на одиничному колі в комплексній площині,
- Таким чином,
- Функція Лобачевського
- Ця функція використовується під час обчислення об'ємів у гіперболічній геометрії, і пов'язана з функцією Клаузена (а отже і з дилогарифмом),
- Іноді використовується інше визначення функції Лобачевського,
- Інтегральний арктангенс
- Виникає під час розгляду дилогарифма уявного аргументу,
- Таким чином,
- Функція Лежандра
- Ця функція виражається через дилогарифми як
- Зокрема, .
Примітки
Посилання
- Leonard Lewin,. Dilogarithms and associated functions. — Macdonald, London, 1958. MR0105524
- Leonard Lewin,. Polylogarithms and associated functions. — North Holland, New York, Oxford, 1981.
- Don Zagier, The dilogarithm function (PDF)
- Weisstein, Eric W. Dilogarithm(англ.) на сайті Wolfram MathWorld.
