Довірча та прогнозна смуги

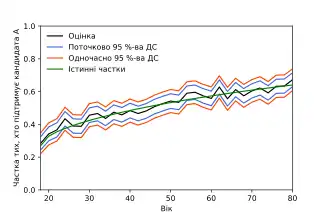
Припустімо, що ми маємо на меті оцінити функцію f(x). Наприклад, f(x) може бути часткою людей певного віку x, які підтримують заданого кандидата на виборах. Якщо x вимірюють із точністю до одного року, ми можемо побудувати окремий 95 %-вий довірчий інтервал для кожного віку. Кожен із цих довірчих інтервалів покриває відповідне істинне значення f(x) із рівнем довіри 0,95. Узяті разом, ці довірчі інтервали складають поточково 95 %-ву довірчу смугу (англ. 95% pointwise confidence band) для f(x).

Мовою математики, поточкова довірча смуга ${\displaystyle {\hat {f}}(x)\pm w(x)}$ з імовірністю покриття 1 − α задовольняє наступну умову окремо для кожного значення x:

${\displaystyle \Pr {\Big (}{\hat {f}}(x)-w(x)\leq f(x)\leq {\hat {f}}(x)+w(x){\Big )}=1-\alpha ,}$

де ${\displaystyle {\hat {f}}(x)}$ є точковою оцінкою f(x).

Імовірністю одночасного покриття (англ. simultaneous coverage probability) набору довірчих інтервалів є ймовірність того, що вони всі покривають свої відповідні істинні значення одночасно. В наведенім вище прикладі ймовірність одночасного покриття є ймовірністю того, що всі інтервали для x = 18, 19, … покривають свої істинні значення (виходячи з того, що 18 є наймолодшим віком, з якого особа може голосувати). Якщо кожен з інтервалів окремо має ймовірність покриття 0,95, то ймовірність одночасного покриття є загалом меншою за 0,95. Одночасно 95 %-ва довірча смуга (англ. 95% simultaneous confidence band) є набором довірчих інтервалів для всіх значень x в області визначення f(x), побудованим таким чином, щоби мати ймовірність одночасного покриття 0,95.

Мовою математики, одночасна довірча смуга ${\displaystyle {\hat {f}}(x)\pm w(x)}$ з імовірністю покриття 1 − α задовольняє наступну умову:

${\displaystyle \Pr {\Big (}{\hat {f}}(x)-w(x)\leq f(x)\leq {\hat {f}}(x)+w(x),\forall {x}{\Big )}=1-\alpha .}$

Майже в усіх випадках одночасна довірча смуга буде ширшою за поточкову довірчу смугу з такою ж імовірністю покриття. У визначенні поточкової довірчої смуги цей квантор загальності пересувається назовні функції ймовірності.

Довірчі смуги для імітованих даних, що зображують частку виборців, що підтримують заданого кандидата на виборах, як функцію від віку виборців. Показано поточково 95 %-ву довірчу смугу та одночасно 95 %-ву довірчу смугу, побудовану із застосуванням поправки Бонферроні.

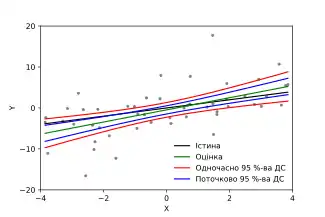
Довірчі смуги зазвичай виникають в регресійнім аналізі.[3] У випадку простої регресії, що включає єдину незалежну змінну, результати може бути подано у вигляді графіку, що показує оцінену лінію регресії разом із або поточковою, або одночасною довірчою смугою. Широко вживаними методами побудови одночасних довірчих смуг у регресії є методи Бонферроні та Шеффе, докладніше див. процедури контролю групової ймовірності помилки першого роду.

Довірчі смуги для простого лінійного регресійного аналізу з використанням імітованих даних. Показано поточково 95 %-ву довірчу смугу та одночасно 95 %-ву смугу, побудовану із застосуванням методу Шеффе.

Довірчі смуги можливо будувати навколо оцінок емпіричної функції розподілу. Проста теорія дозволяє будувати поточкові довірчі інтервали, але можливо також будувати й одночасну довірчу смугу для функції розподілу ймовірності як цілого, обертаючи критерій Колмогорова — Смирнова, або використовуючи непараметричні правдоподібнісні методи.[4]

Довірчі смуги виникають, коли статистичний аналіз зосереджується на оцінюванні функції.

Було також розроблено довірчі смуги для оцінок функцій густини, функцій спектральної густини,[5] функцій квантилів, згладжувань розсіювань, функцій виживаності та характеристичних функцій.^{[джерело?]}

Прогнозні смуги пов'язано з прогнозними інтервалами[6] так само, як довірчі смуги пов'язано з довірчими інтервалами. Прогнозні смуги зазвичай виникають у регресійнім аналізі. Метою прогнозної смуги є покрити з приписаною ймовірністю значення одного або більше майбутніх спостережень з тієї ж генеральної сукупності, з якої було вибрано задані дані. Як і прогнозні інтервали є ширшими за довірчі інтервали, так і прогнозні смуги будуть ширшими за довірчі смуги.

Мовою математики, прогнозна смуга ${\displaystyle {\hat {f}}(x)\pm w(x)}$ з імовірністю покриття 1 − α задовольняє наступну умову для кожного значення x:

${\displaystyle \Pr {\Big (}{\hat {f}}(x)-w(x)\leq y^{*}\leq {\hat {f}}(x)+w(x){\Big )}=1-\alpha ,}$

де y^* є спостереженням, узятим із процесу породжування даних у заданій точці x, що не залежить від даних, використаних для побудови точкової оцінки ${\displaystyle {\hat {f}}(x)}$ та довірчого^{[прояснити: ком.]} інтервалу w(x). Це — поточковий прогнозний інтервал.^{[прояснити: ком.]} Можливо було би побудувати й одночасний інтервал^{[прояснити: ком.]} для скінченного числа незалежних спостережень, застосовуючи, наприклад, метод Бонферроні для розширювання інтервалу^{[прояснити: ком.]} на відповідну величину.