Емпірична функція розподілу

Емпірична функція розподілу — це функція розподілу реалізації випадкової величини, яку будують за результатами вимірювань (спостережень).

Синя лінія показує емпіричну функцію розподілу. Сірі стовпчики представляють зразки, які відповідають емпіричній функції розподілу, а зелена крива є справжньою функцію накопиченого розподілу.

Нехай маємо випадкову величину ${\displaystyle \xi :x_{1},x_{2},\ldots ,x_{n}}$, де n — загальна кількість спостережень. Через ${\displaystyle v_{k}(x)}$ позначимо випадкову величину, яка дорівнює кількості елементів вибірки ${\displaystyle \xi }$ значення яких менше x. Тоді емпірична функція розподілу буде задаватись як ${\displaystyle {\hat {F}}_{k}(x)={\frac {v_{k}(x)}{n}}}$.

Для побудови таблиці значень емпіричної функції розподілу використовують такий метод. Спочатку всі результати спостережень впорядковують за зростанням й визначають їх ранги (порядкові номера в отриманої послідовності). Потім кожному спостереженню приводять у відповідність число ${\displaystyle {\hat {F}}_{k}(x)={\frac {x_{k}}{n}}}$.

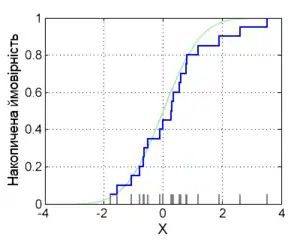
Графік емпіричної функції розподілу має східчастий вигляд. Із збільшенням кількості спостережень він стає гладкішим, а емпірична функція розподілу наближається до теоретичної функції розподілу генеральної сукупності чи певної теоретичної моделі розподілу.

Емпіричні функції розподілу широко використовують у непараметричних статистичних критеріях (омега-квадрат, Колмогорова — Смирнова тощо).