Діаграма Найквіста

Діаграма Найквіста, також Амплітудно-фазова частотна характеристика (АФЧХ) — це годограф кінця вектора K(jω) на комплексній площині при різних значеннях частоти ω, яка змінюється в межах від 0 до нескінченності.

Діаграма Найквіста

Загальний опис

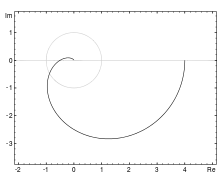
Амплітудно-фазова частотна характеристика – це лінія, що з’єднує кінці радіус-векторів, довжина яких дорівнює відношенню амплітуди вихідної і вхідної величин, а кут, утворений з додатним напрямком дійсної осі дорівнює різниці фаз вихідної і вхідної величин для частот, що змінюються від 0 до ∞.

АФЧХ- зручне представлення частотного відгуку лінійної стаціонарної динамічної системи у вигляді графіка в комплексних координатах. На такому графіку частота виступає в якості параметра кривої, фаза і амплітуда системи на заданій частоті представляється кутом і довжиною радіус-вектора кожної точки характеристики. По суті такий графік об'єднує на одній площині амплітудно-частотну і фазо-частотну характеристики.

Термін вживається також в застосуванні до передавальної функції системи, записаної у вигляді перетворення Фур'є вихідного сигналу, поділеного на перетворення Фур'є вхідного сигналу.

Приклад АФЧХ

Назва

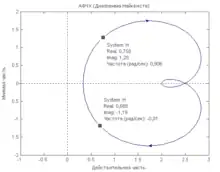
У російській літературі для графіка прийнято назву АФЧХ (або АФХ). На заході АФЧХ називають діаграмою Найквіста або годографом Найквіста (англ. Nyquist Plot), по імені видатного інженера Гаррі Найквіста. Якщо ж термін АФЧХ використовується в застосуванні до передавальної функції системи, його називають частотним відгуком (англ. Frequency response).

Використання

В теорії ланцюгів діаграма Найквіста використовується для графічного уявлення частотних властивостей ланцюгів. АФЧХ застосовується в основному для аналізу систем, зокрема дослідження системи на стійкість і її запасів. АФЧХ є класичним засобом аналізу стійкості лінійних систем. Існує безліч програмних продуктів, що дозволяють проводити дослідження на стійкість частотними методами.

Застосовується у теорії автоматичного керування при визначенні стійкості систем.

Див. також

Література

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.