Теорія лінійних стаціонарних систем

Визначальними властивостями будь-якої лінійної стаціонарної системи є лінійність і стаціонарність:

• Лінійність означає лінійний зв'язок між входом і виходом системи.

Формально, лінійною називається система, що має таку властивість:

якщо сигнал на вході системи можна подати зваженою сумою впливів (наприклад, двох) — :: ${\displaystyle x(t)=Ax_{1}(t)+Bx_{2}(t)}$

то сигнал на виході системи є також зваженою сумою реакцій на кожен із впливів — :: ${\displaystyle y(t)=Ay_{1}(t)+By_{2}(t)}$

для будь-яких сталих A і B.

• Стаціонарність — означає, що вихідний сигнал системи як реакція на будь-який заданий вхідний сигнал однаковий для будь-якого моменту прикладення вхідного сигналу (з точністю до часу запізнювання моменту прикладення вхідного сигналу). У вужчому сенсі — при запізненні вхідного сигналу за часом на деяку величину, вихідний сигнал буде запізнюватися на ту ж саму величину.

Динаміку системи, що має перераховані вище властивості, можна описати однією простою функцією, наприклад, імпульсною перехідною функцією. Вихід системи можна розрахувати як згортку вхідного сигналу з імпульсною перехідною функцією системи. Цей метод аналізу іноді називають аналізом у часовій області. Сказане справедливе і для дискретних систем.

Зв'язок між часовою і частотною областями

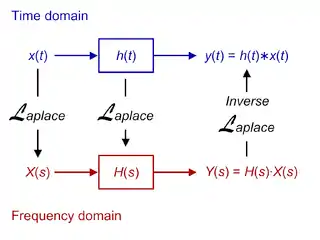
Крім того, будь-яку ЛСС можна описати в частотній області за допомогою її передавальної функції, яка є перетворенням Лапласа імпульсної перехідної функції (або Z-перетворенням у разі дискретних систем). У силу властивостей цих перетворень, вихід системи в частотній області дорівнюватиме добутку передавальної функції і відповідного перетворення вхідного сигналу. Іншими словами, згортці в часовій області відповідає множення в частотній області.

Для всіх ЛСС власні функції є комплексними експонентами. Тобто, якщо вхід системи є комплексним сигналом ${\displaystyle A\exp({st})}$ з деякою комплексною амплітудою ${\displaystyle A}$ і частотою ${\displaystyle s}$, то вихід дорівнюватиме деякому сигналу ${\displaystyle B\exp({st})}$ з комплексною амплітудою ${\displaystyle B}$. Відношення ${\displaystyle B/A}$ буде передавальною функцією системи на частоті ${\displaystyle s}$.

Оскільки синусоїда є сумою комплексних експонент з комплексно-спряженими частотами, якщо вхід системи — синусоїда, то виходом системи буде також синусоїда, в загальному випадку з іншого амплітудою і фазою, але з тією ж частотою.

Теорія ЛСС добре підходить для опису багатьох систем. Більшість ЛСС значно простіше аналізувати, ніж нестаціонарні і нелінійні системи. Будь-яка система, динаміка якої описується лінійним диференціальним рівнянням зі сталими коефіцієнтами, є лінійною стаціонарною системою. Прикладами таких систем є електричні схеми, зібрані з резисторів, конденсаторів і котушок індуктивності (RLC-ланцюжки). Вантаж на пружині також можна вважати ЛСС.

Більшість загальних концепцій ЛСС схожі як у разі неперервних систем, так і в разі дискретних систем.

Розглянемо нестаціонарну систему, чия імпульсна характеристика є функцією двох змінних. Подивимося, як властивість стаціонарності допоможе нам позбутися від одного виміру. Наприклад, нехай вхідний сигнал — ${\displaystyle x(t)}$, де аргумент — числа дійсної осі, тобто ${\displaystyle t\in \mathbb {R} }$. Лінійний оператор ${\displaystyle {\mathcal {H}}}$ показує, як система відпрацьовує цей вхідний сигнал. Відповідний оператор для деякого набору аргументів є функцією двох змінних:

${\displaystyle h(t_{1},t_{2}){\mbox{, }}t_{1},t_{2}\in \mathbb {R} .}$

Для дискретної системи:

${\displaystyle h[n_{1},n_{2}]{\mbox{, }}n_{1},n_{2}\in \mathbb {Z} .}$

Оскільки ${\displaystyle {\mathcal {H}}}$ — лінійний оператор, вплив системи на вхідний сигнал ${\displaystyle x(t)}$ подається лінійним перетворенням, описуваним таким інтегралом (інтеграл суперпозиції)

${\displaystyle y(t_{1})=\int \limits _{-\infty }^{\infty }h(t_{1},t_{2})\,x(t_{2})\,dt_{2}.}$

Якщо лінійний оператор ${\displaystyle {\mathcal {H}}}$ до всього іншого є і стаціонарним, тоді

${\displaystyle h(t_{1},t_{2})=h(t_{1}+\tau ,t_{2}+\tau )\qquad \forall \,\tau \in \mathbb {R} .}$

Поклавши

${\displaystyle \tau =-t_{2},}$

отримаємо:

${\displaystyle h(t_{1},t_{2})=h(t_{1}-t_{2},0).}$

Для стислості запису другий аргумент в ${\displaystyle h(t_{1},t_{2})}$ зазвичай опускають і інтеграл суперпозиції стає інтегралом згортки:

${\displaystyle y(t_{1})=\int \limits _{-\infty }^{\infty }h(t_{1}-t_{2})\,x(t_{2})\,dt_{2}=(h*x)(t_{1}).}$

Таким чином, інтеграл згортки показує як лінійна стаціонарна система відпрацьовує будь-який вхідний сигнал. Отримане співвідношення для дискретних систем:

${\displaystyle y[n_{1}]=\sum _{n_{2}=-\infty }^{\infty }h[n_{1}-n_{2}]\,x[n_{2}]=(h*x)[n_{1}].}$

Якщо до входу системи прикласти вхідний сигнал у вигляді дельта-функції Дірака, кінцевий вихідний сигнал ЛСС являтиме собою імпульсну перехідну функцію системи. Запис:

${\displaystyle (h*\delta )(t)=\int \limits _{-\infty }^{\infty }h(t-\tau )\,\delta (\tau )\,d\tau =h(t),}$

Для дискретної системи:

${\displaystyle x[n]=\sum _{m=-\infty }^{\infty }x[m]\delta [n-m].}$

(через властивості зсуву дельта-функції).

Зауважимо, що:

${\displaystyle h(t)=h(t,0)\ ({\mbox{with }}t=t_{1}-t_{2})}$

тобто ${\displaystyle h(t)}$ — імпульсна перехідна функція системи.

Імпульсна перехідна функція використовується для того, щоб знайти вихідний сигнал системи як реакцію на будь-який вхідний сигнал. Крім того, будь-який вхід можна подати у вигляді суперпозиції дельта-функцій:

${\displaystyle x(t)=\int \limits _{-\infty }^{\infty }x(\tau )\delta (t-\tau )\,d\tau }$

Приклавши до входу системи, отримаємо:

${\displaystyle {\mathcal {H}}x(t)={\mathcal {H}}\int \limits _{-\infty }^{\infty }x(\tau )\delta (t-\tau )\,d\tau }$

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }{\mathcal {H}}x(\tau )\delta (t-\tau )\,d\tau }$ (оскільки ${\displaystyle {\mathcal {H}}}$ лінійна)

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }x(\tau ){\mathcal {H}}\delta (t-\tau )\,d\tau }$ (оскільки ${\displaystyle x(\tau )}$ стала за t і ${\displaystyle {\mathcal {H}}}$ лінійна)

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }x(\tau )h(t-\tau )\,d\tau }$ (за визначенням ${\displaystyle h(t)}$)

В імпульсній перехідній функції ${\displaystyle h(t)}$ міститься вся інформація про динаміку ЛСС.

Власна функція — функція, для якої вихід оператора являє собою ту ж функцію, в загальному випадку з точністю до сталого множника. Запис:

${\displaystyle {\mathcal {H}}f=\lambda f}$ ,

де f — власна функція, і ${\displaystyle \lambda }$ — власне число, стала.

Експоненти ${\displaystyle e^{st}}$, де ${\displaystyle s\in \mathbb {C} }$ є власними функціями лінійного стаціонарного оператора.

${\displaystyle H(s)={\mathcal {L}}\{h(t)\}=\int \limits _{-\infty }^{\infty }h(t)e^{-st}dt}$

є точним способом отримати власні числа з імпульсної перехідної функції. Особливий інтерес становлять чисті синусоїди, тобто експоненти вигляду ${\displaystyle \exp({j\omega t})}$ де ${\displaystyle \omega \in \mathbb {R} }$ і ${\displaystyle j}$ — уявна одиниця. Їх зазвичай називають комплексними експонентами, навіть якщо аргумент не має дійсної частини. Перетворення Фур'є ${\displaystyle H(j\omega )={\mathcal {F}}\{h(t)\}}$ дає власні числа для чисто комплексних синусоїд. ${\displaystyle H(s)}$ називається передавальною функцією системи, іноді в літературі цей термін застосовують і до ${\displaystyle H(j\omega )}$.

Перетворення Лапласа зазвичай використовують для односторонніх сигналів, тобто за нульових початкових умов. Початковий момент часу без втрати загальності приймається за нуль, а перетворення береться від нуля до нескінченності (перетворення, яке виходить при інтегруванні також і до мінус нескінченності, називається двостороннім перетворенням Лапласа).

Перетворення Фур'є використовується для аналізу систем, через які проходять періодичні сигнали, і в багатьох інших випадках — наприклад, для аналізу системи на стійкість .

Через властивості згортки для обох перетворень мають виконуються співвідношення:

${\displaystyle y(t)=(h*x)(t)=\int \limits _{-\infty }^{\infty }h(t-\tau )x(\tau )d\tau }$

${\displaystyle \quad ={\mathcal {L}}^{-1}\{H(s)X(s)\}}$

Для дискретних систем:

${\displaystyle y[n]=(h*x)[n]=\sum _{m=-\infty }^{\infty }h[n-m]x[m]}$

${\displaystyle \quad ={\mathcal {Z}}^{-1}\{H(s)X(s)\}}$

Деякі з важливих властивостей будь-якої системи — причинність і стійкість. Для того, щоб система існувала в реальному світі, має виконуватися принцип причинності. Нестійкі системи можуть бути побудованими і іноді навіть бути корисними.

• АФЧХ
• ЛАФЧХ
• Системний аналіз
• Передавальна функція
• Функція Гріна
• Нелінійне керування

• P. P. Vaidyanathan and T. Chen. Role of anticausal inverses in multirate filter banks -- Part I: system theoretic fundamentals // IEEE Trans. Signal Proc. : journal. — 1995. — 5.
• P. P. Vaidyanathan and T. Chen. Role of anticausal inverses in multirate filter banks -- Part II: the FIR case, factorizations, and biorthogonal lapped transforms // IEEE Trans. Signal Proc. : journal. — 1995. — 5.
• В.И. Зубов. Теория уравнений управляемого движения. — Л. : ЛГУ, 1980.